概述

传统的神经网络的全连接层(full connected)在遭遇较大的输入数据时，需要训练的参数将会非常多。举个例子，一张1000×1000的图片，作flatten处理后就有了1000×1000×3的输入维度，如果第二层的隐藏单元数是1000，参数W的维度就是3000000×1000。
参数过多，就意味着训练难度变高。在这种情况下，卷积神经网络就诞生了。

什么是卷积

我们先来看一下最基础的一点：什么是卷积？

用一个例子来进行说明，假如我们有一张6×6的图片，为了方便理解，我们暂时假定它第三个维度为1，即通道数为1。那么一次卷积操作如下：

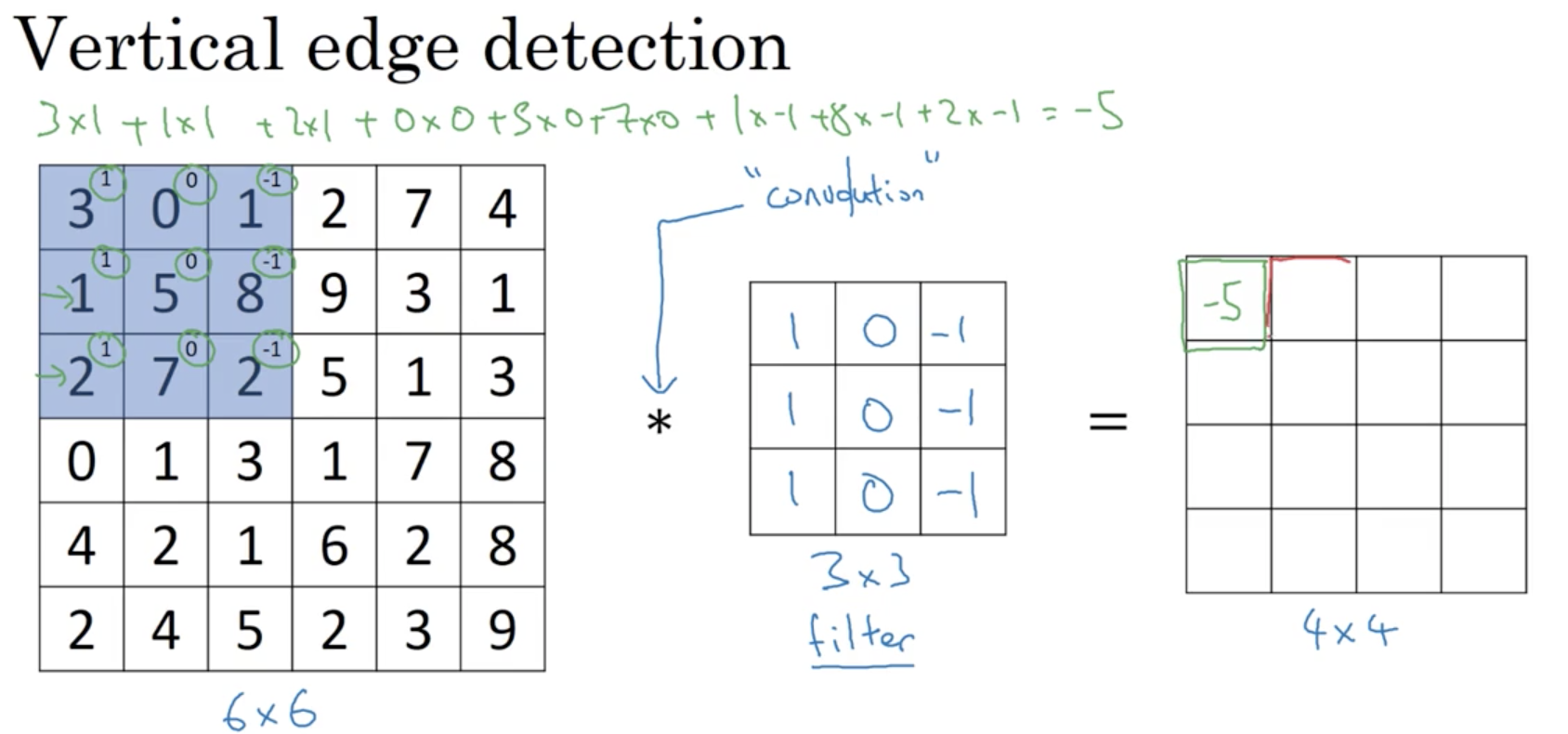
如上图所示，左一的6×6矩阵代表我们的输入矩阵，中间的3×3矩阵叫做过滤器(filter)，也叫做卷积核，而二者中间的”*“就表示卷积，它和计算机中的乘法符号一致。

卷积的运算方法就是 从输入矩阵的左上角开始，从左到右每一次取出一个与卷积核维度一样大小的矩阵，这里是3×3。 将取出的矩阵的每一位与卷积核对应为相乘并相加，得到的数据填在右侧结果矩阵的对应位置。

第二步如下：

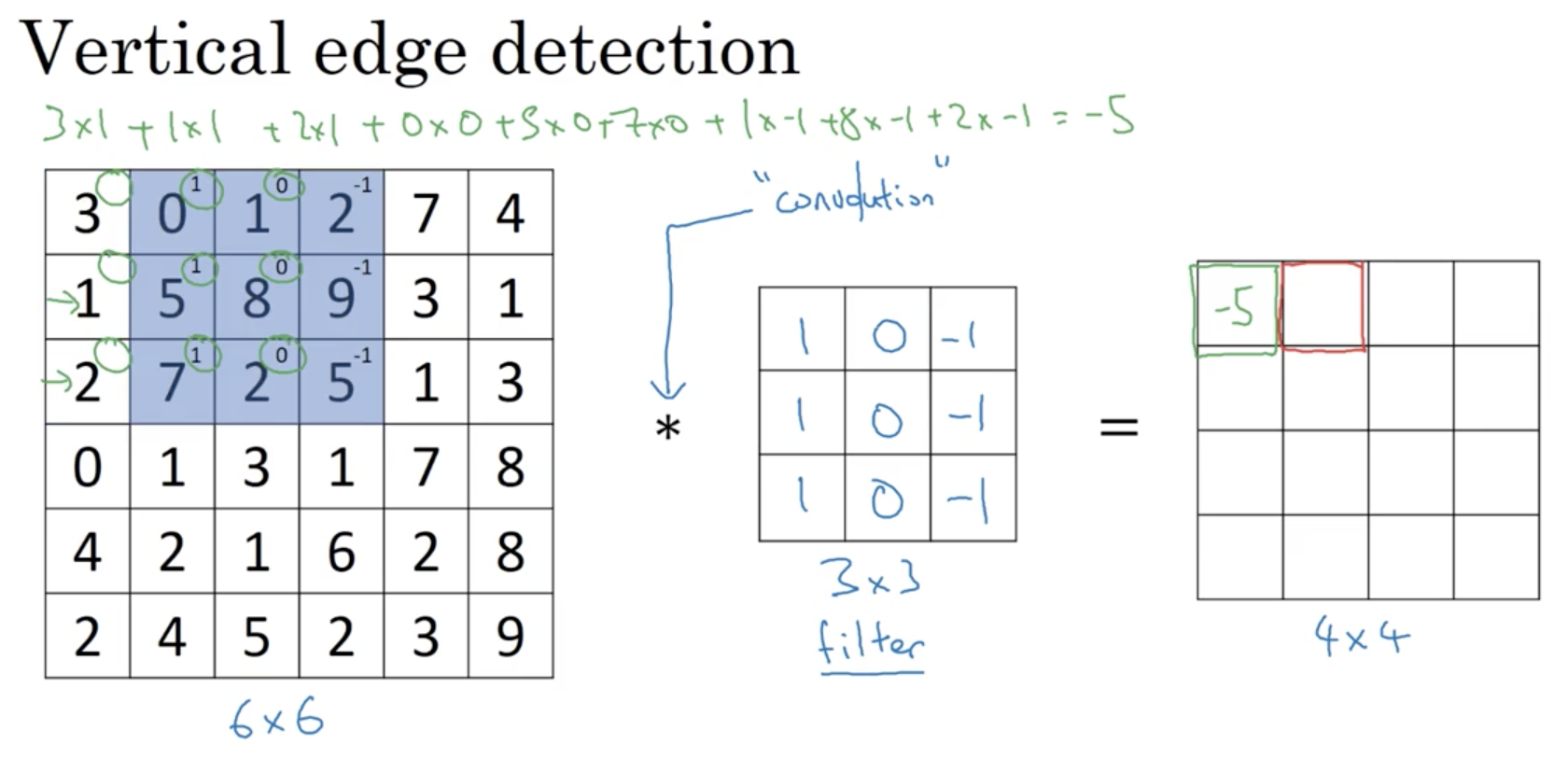
以此类推，往右不能再走时，就向下移动一行，再次从最左边开始取。
这样，最终我们可以得到一个4×4的结果矩阵(一张变小的图片)。

卷积在做什么

你可能会感到困惑，这样的一步所谓的操作到底做了些什么。
就我们上面的例子来说，这样一个卷积核的效果可以用六个字来概括：“垂直边缘检测”。
如下：

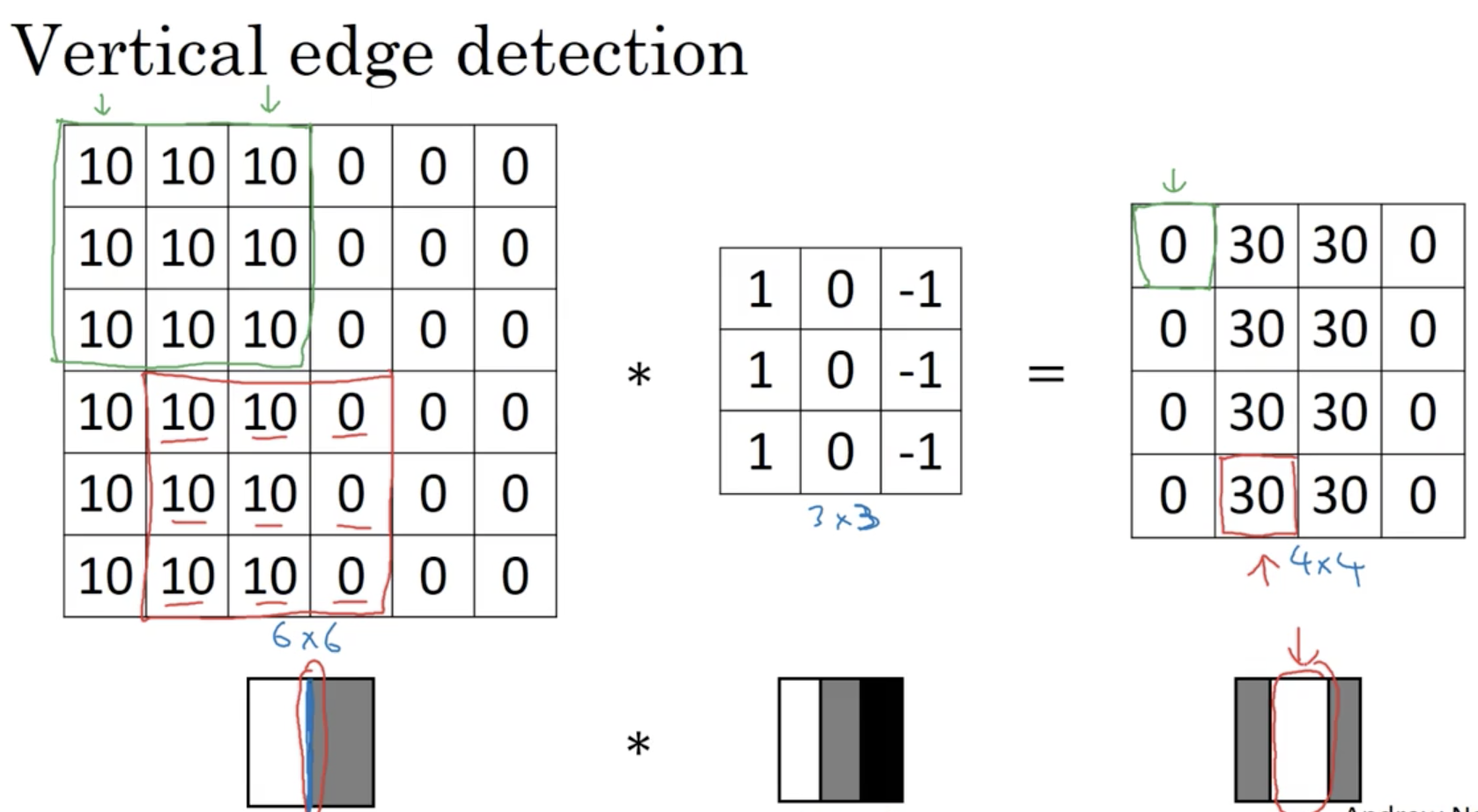
可以看到，结果图片的中部有一道明显的白色，这就是检测出来的垂直边缘。是的，它看起来与左边的输入图片有些不符合，显得比较厚，这是因为我们选择的图片较小(才6×6)，当把图片变大时，结果就变得较为可观了。

既然有垂直边缘检测的卷积核，自然就有其它功能的卷积核，比如水平边缘检测卷积核，比如着重突出某些边缘特征的卷积核等。

而卷积核的值是可以通过训练得到的，这点我们将在后面介绍。

填充-padding

除了卷积，conv网络的第二个重要的积木就是填充。

在上一节介绍卷积时，一个6×6的图片经过一次卷积操作变成了4×4，可见卷积操作是会让输入数据的维度降低的。这样的操作多来几次，再大的图片也遭不住。因此，为了构建深层网络，填充就必不可少。

首先，关于卷积操作减小维度，是有一个通用的计算公式的：
结果矩阵的维度 = (n-f+1) × (n-f+1)
其中f为卷积核的维度，n为输入矩阵的维度。

除了会减小图片的维度外，卷积还会导致图片角落的像素只能被使用到一次，而中间的数据则会被使用多次，这样会导致图片边缘的数据不能得到足够的利用，甚至被丢失了。

所以所谓填充，就是填充数据的边缘：

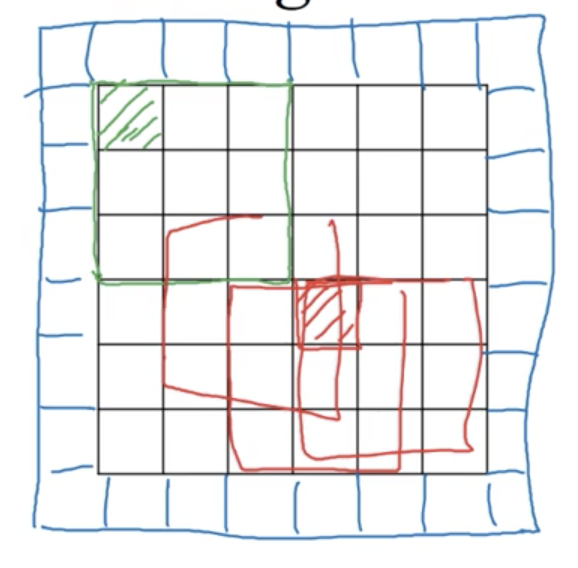
通过在原图片边缘填充一层使之变成8×8的图像，从而经过卷积操作后，你依然可以得到一个6×6的图像。

一般来说，在卷积网络中大多数时候使用这样的填充，即使数据在填充后进行卷积得到与原数据同样维度的数据。这样的卷积操作我们称之为same卷积。

除此之外还有full卷积和valid卷积，前者让图像最角落的元素也可以被充分利用，而后者则是不做填充。

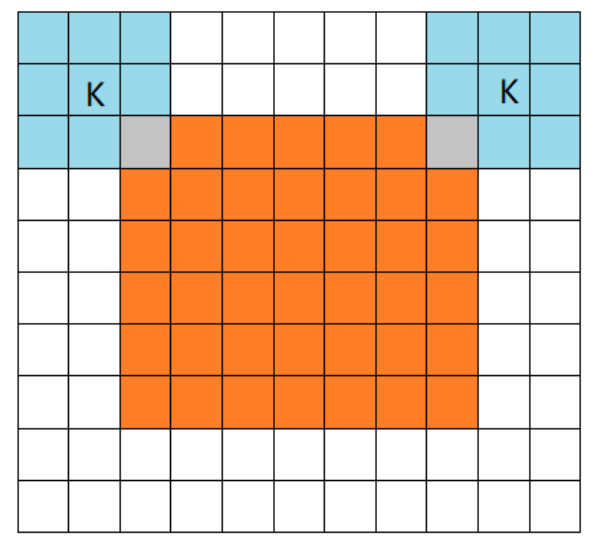
上图为full卷积

步幅(stride)卷积

在之前的介绍中，我们每次计算卷积后，都是在原图片上向右或者向下移动一步。而步幅卷积，顾名思义，就是将这个一步扩展开来，每次移动s步，我们以2为例：

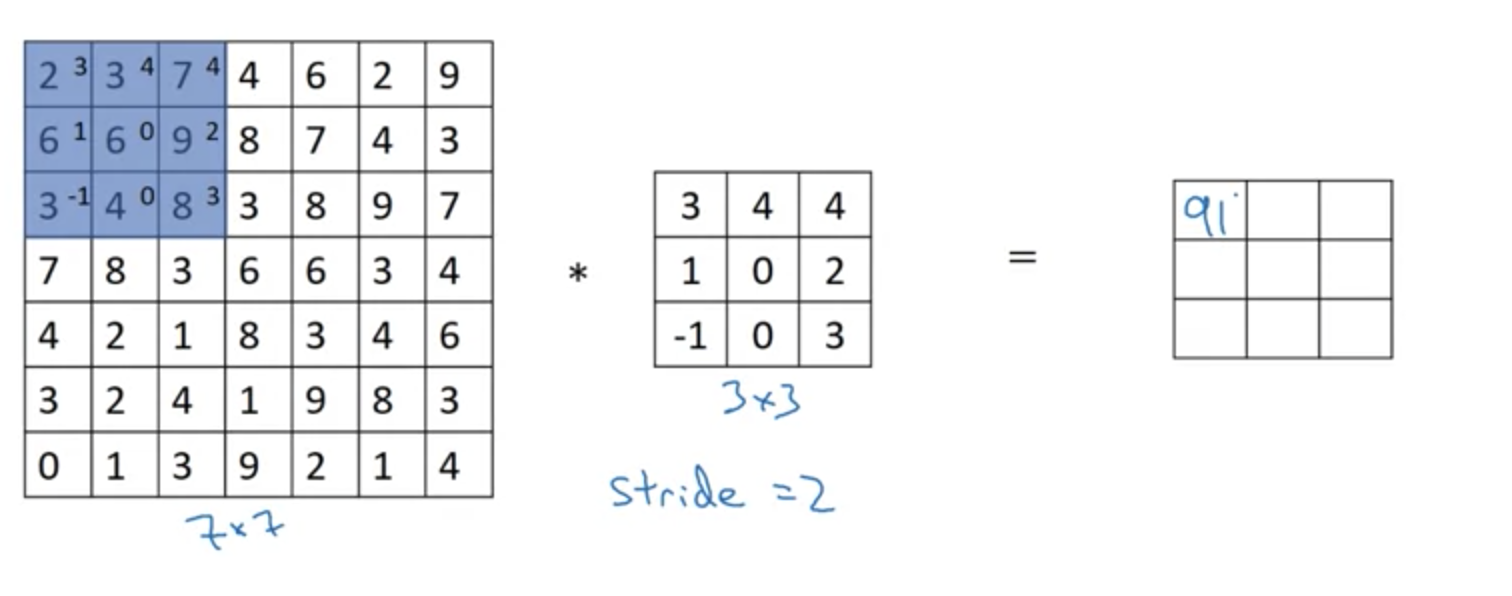
如上为第一步和第二步，此外，当需要向下移动时，也是移动s步

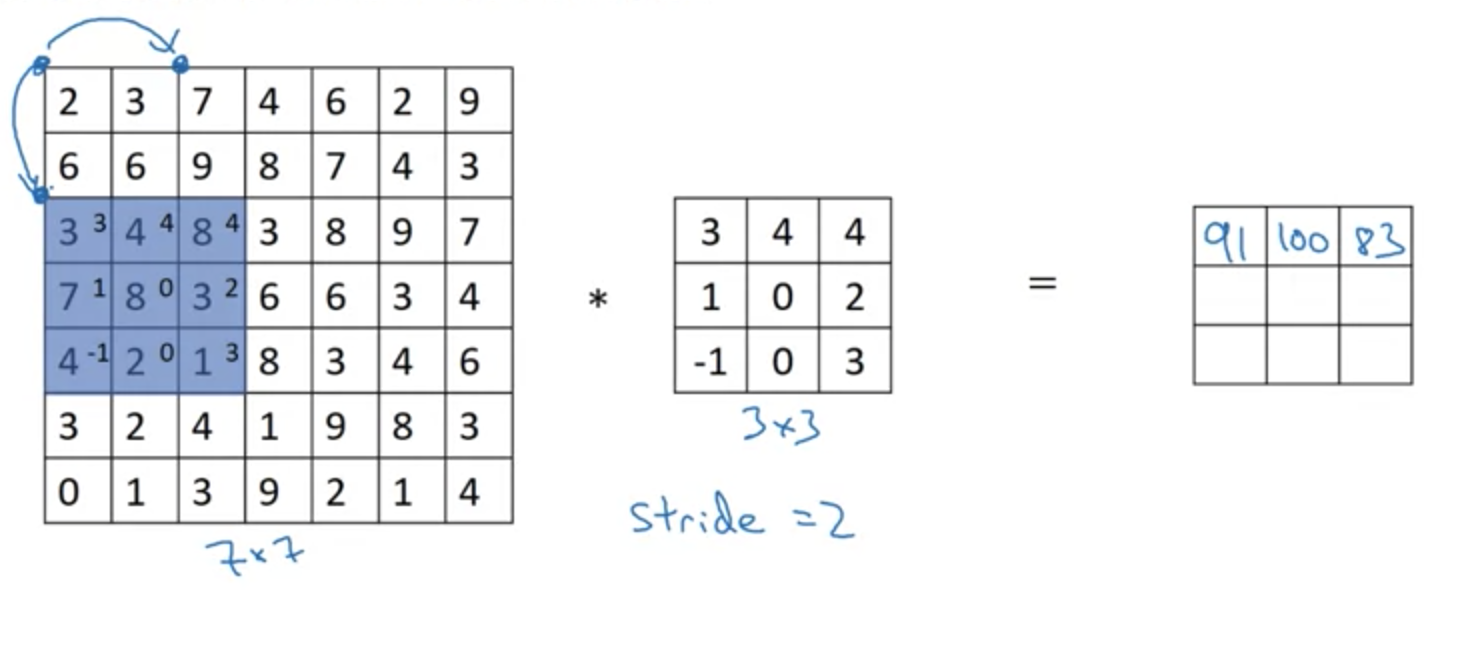
容易计算，经过步幅为s的卷积后，结果矩阵维度的计算方式为：

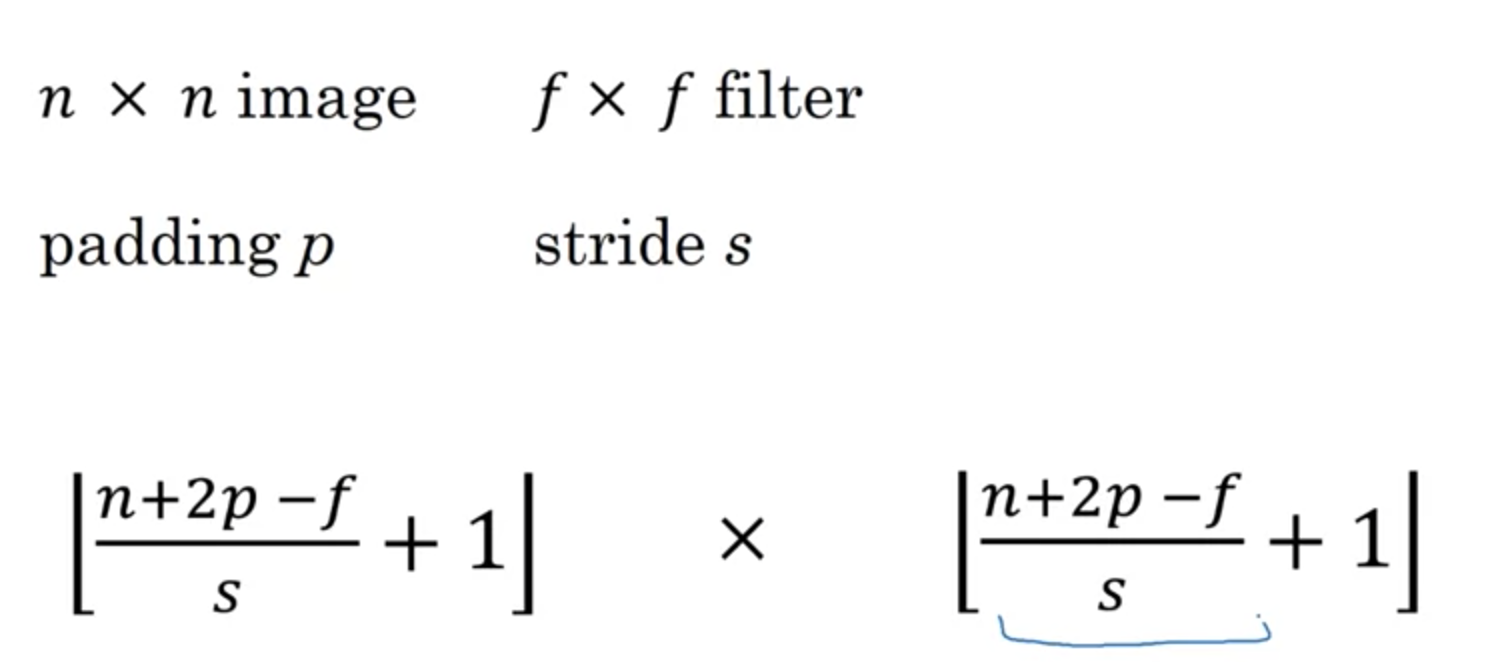
假如当向右移动s步已经超出了原矩阵范围，即当不能被整除的时候，就直接舍弃剩余部分直接向下走了。即向下取整。

三维数据的卷积

对于现实情况中的图片来说，因为RGB格式的存在，我们的输入数据大多都是3维的，那么，如何将卷积扩展到三维数据上去呢？

首先，卷积核（过滤器）也要变成三维，且第三个维度要和原矩阵相同(第三个维度在卷积中我们一般叫做通道)，如下：

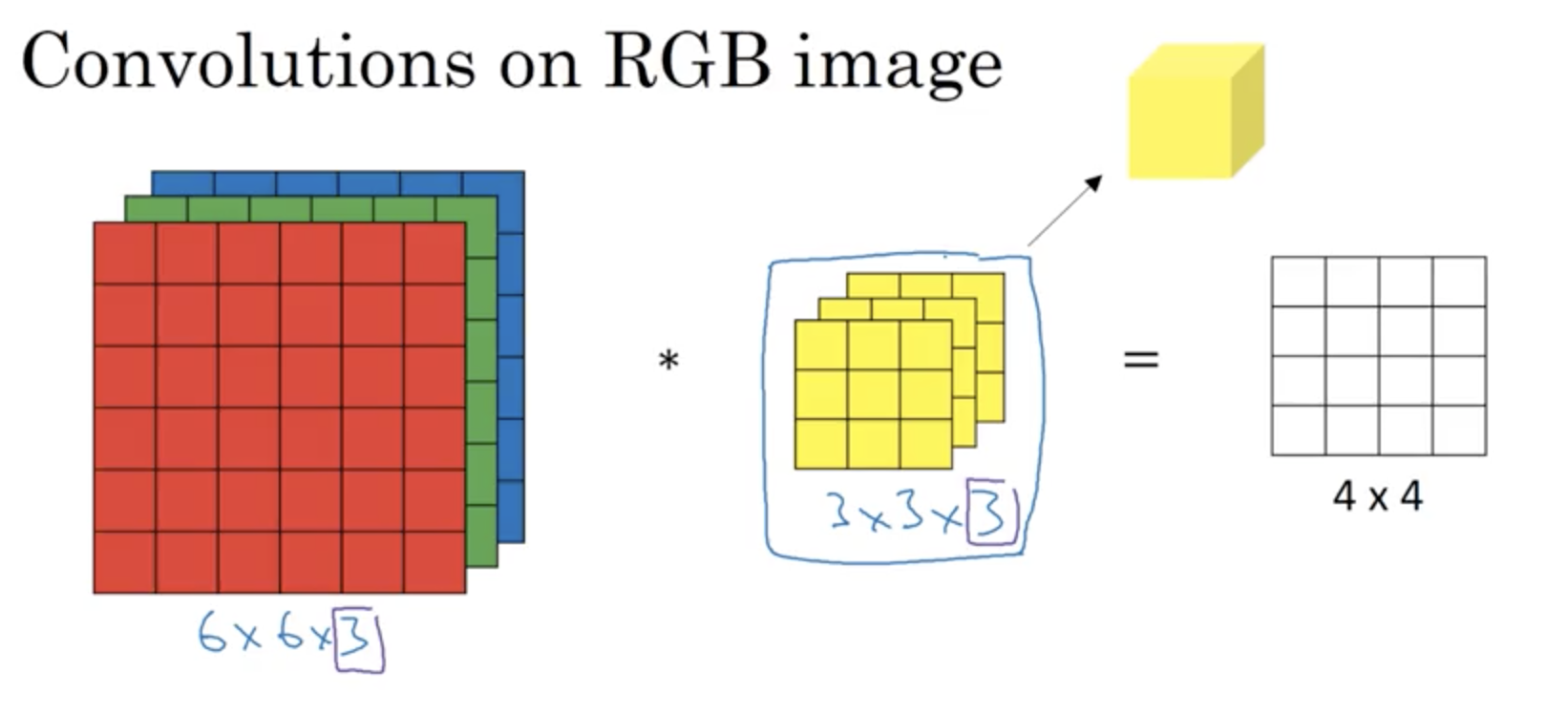
可以看到，最终的结果是一个4*4的矩阵，没有了第三个维度，计算方法其实很简单，基本就是二维计算方式的三维扩展：

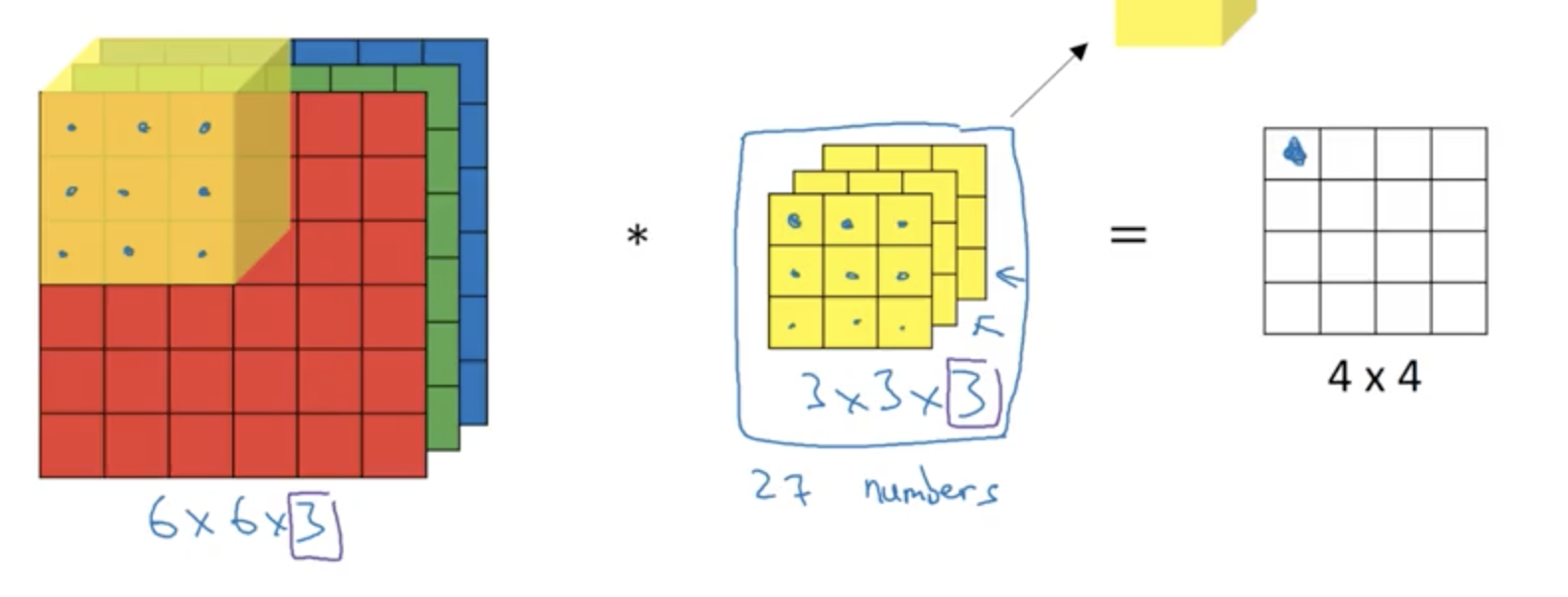
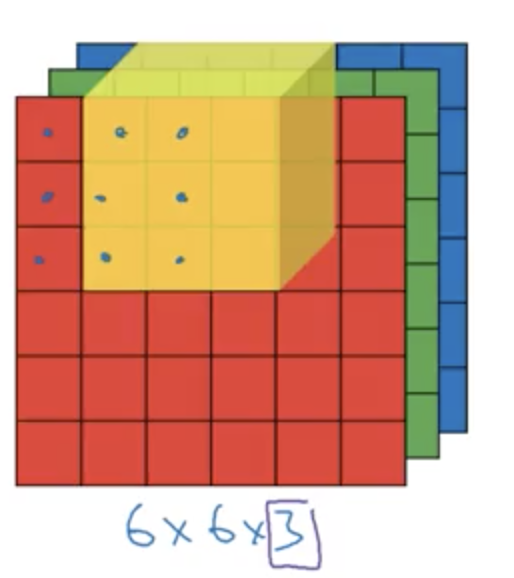
即把每个3×3×3 = 27个格子的数字对应相乘并相加，然后右移和下移即可，因为深度一致，并不需要关心第三个维度。

卷积核的设计很灵活，假如你把卷积核的第二层和第三层都设置为0，相当于在结果矩阵中就只有你对第一层的卷积，在RGB图片中，你就只检测了红色通道的边缘。

更常用的是，你可以同时使用多个卷积核，然后把得到的结果堆叠，得到通道数大于1的结果：

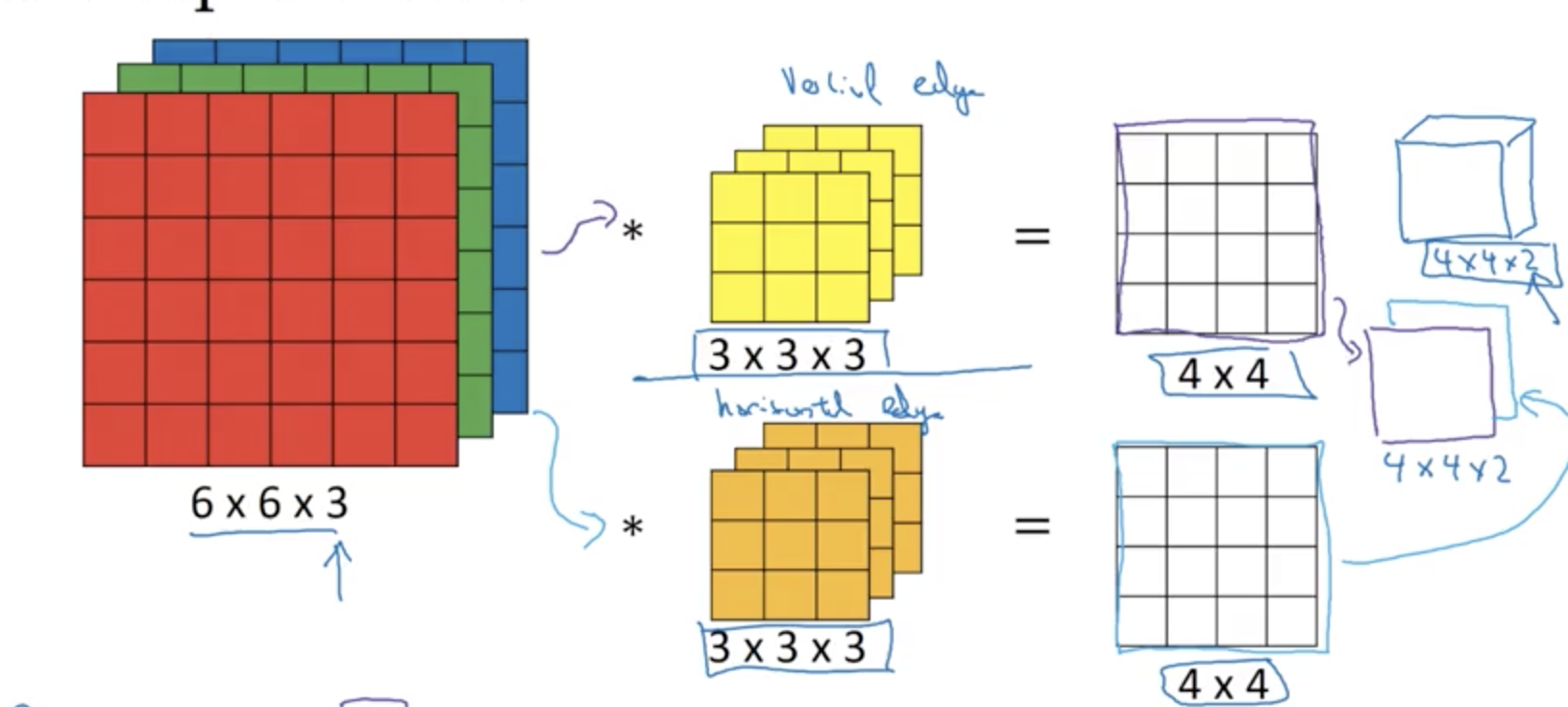
所以卷积结果矩阵的通道数，取决于卷积核的数量，记住这一点。

卷积神经网络

介绍了这么多，我们拉通来看一下，把上述知识点结合起来，就是卷积神经网络的一层：

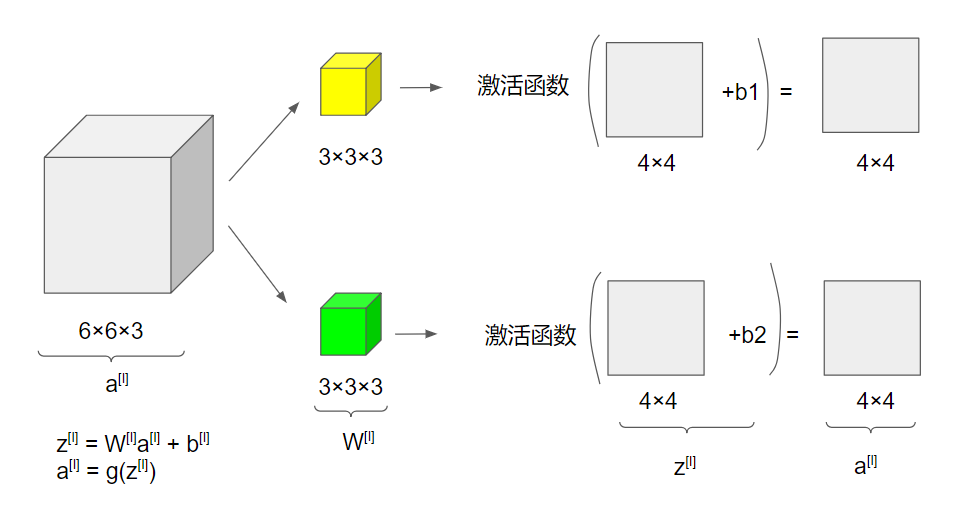
之前我们说过，每一个过滤器(卷积核)都相当于是过滤出原数据的一个特性。上图中，用了2个过滤器，将每个过滤器得到的结果再进行一次激活。激活函数可以说是神经网络中的一种重要工具，一般是一个非线性函数，可以简单地理解为将数据中的特点放大并且保证了多层网络的实用性。激活之后再重叠在一起，就得到了我们最后4×4×2的结果。

如果你知道普通神经网络的结构，它每一层的运算就是先进行 z[l] = W*a[l-1] + b[l]，再进行 a[l] = g(z[l])。可以看到对于我们的卷积神经网络，这一层的操作，也可以对应成这个公式，过滤器就是我们的W。

既然过滤器是我们W，上面我们也说过过滤器的值可以训练，那么这么一层卷积网络，我们需要训练多少参数呢？
假设我们有10个3×3×3的过滤器，那么我们需要 3×3×3×10 + 10(b参数，偏差值) 个，即280个参数。

ConvNet中的符号

在卷积网络中，你会看到很多各种符号以及参数、中间值，结果的维度，我们稍作总结：

以上就是卷积网络中的一层了，那么我们如何扩展它来构建一个卷积网络呢？

PS: ConvNet是卷积神经网络的简写

一个简单的例子

现在假如你有一些照片，你想通过卷积网络来实现图片的分类，假如输入图片的大小为39×39×3：

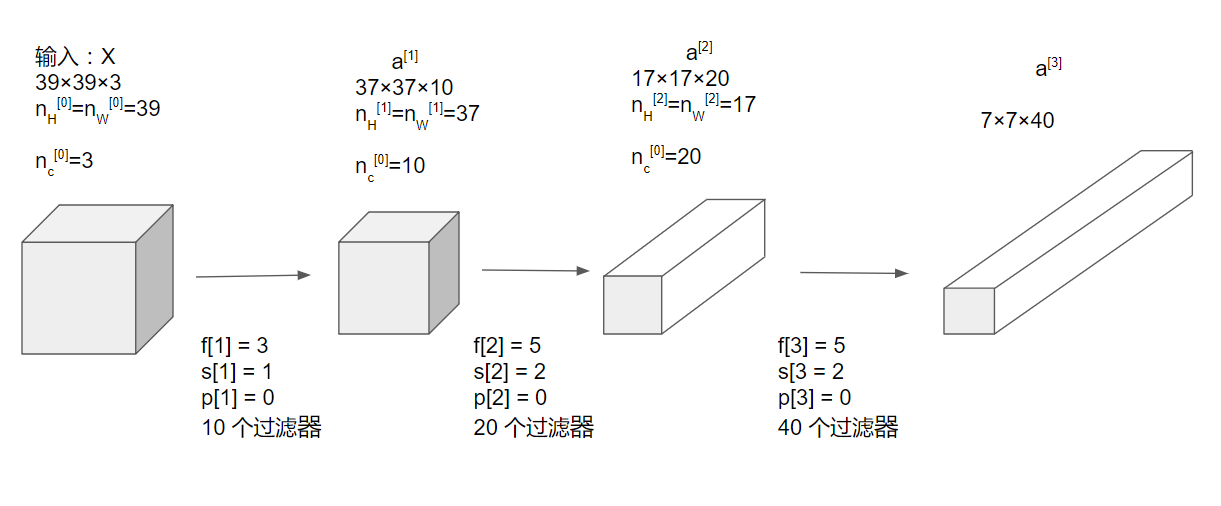
接着，我们可以把最后这个7×7×40的矩阵展开成1960的向量，接着我们可以使用普通神经网络的手段，使用逻辑回归或者一个softmax层来进行最后结果的计算。

从上面可以看出一个大多数卷积神经网络的趋势，即随着层数的增加，矩阵的宽高会逐渐减小，而通道数量会逐渐增加。

其它的层类型

上面的网络中，这些使用卷积核的层都可以叫做卷积层，但神经网络层中还有一些其他的层类型，比如池化(pooling)层，全连接(full connect/FC)层等。
将卷积层与这二者结合，我们可以搭建出更好的卷积神经网络。

池化层

在ConvNet中，经常会使用一种叫做池化层(pooling layer)的结构来减小表示层的大小，从而加快模型训练，甚至更好的发现一些特性。

下面介绍两种池化层

最大值(Max)池化

非常简单，如下：

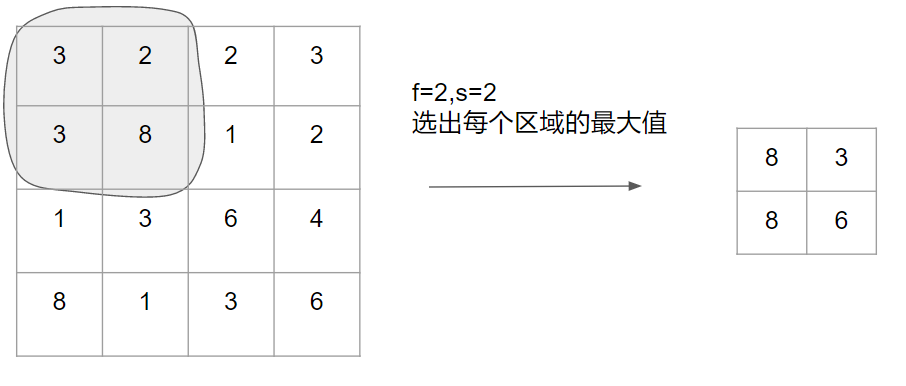
虽然很简单，但max池化在很多的实际应用中都有很好的效果。为什么呢？
直白的理解一下，加入你把这个4×4的区域看作某个特征的集合，即神经网络某个层中的激活状态，那么一个大的数字意味着算法可能检测到了一个特定的特征，如上图左上的2*2区域就有这样的特征，8被挑选并保留下来，它可能是一个垂直边缘，可能是一个任何难以描述的特征，而右上区域没有这样的特征，它的最大值依然很小。
所以，max pooling作所做的其实是 ，如果在过滤器中任何地方检测到了任何特征，就保留最大的数值。
反之，如果没有明显的特征被检测到，比如右上方的四分之一区域就没有这个特征，在结果中那些数值的最大值仍然相当小。

平均值池化

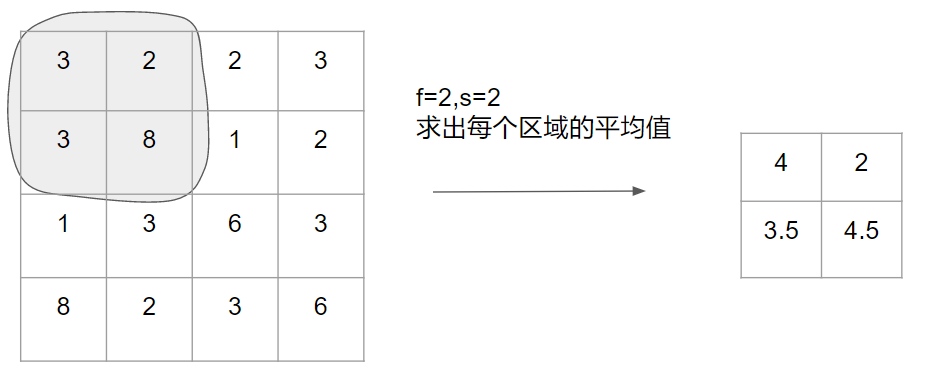
就不介绍了…

池化层特点

最大值池化的使用通常比均值池化多得多。
也许你注意到了，大多数池化层都不需要学习超参数，只要确定了f和s，计算就确定了。
而且如果输入数据是3维的，则结果中通道数量依然保持，即每一层都像第一层一样进行过滤。

卷积网络样例

todo…

卷积为什么有用

比起一般的全连接神经网络，卷积神经网络主要有2个优势，参数共享和连接稀疏性。

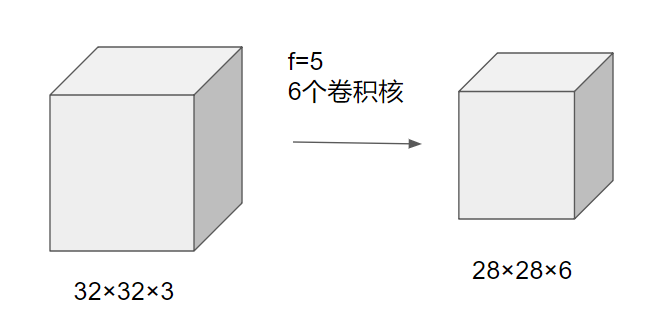
举个例子，如上图，第一层共32×32×3 = 3072个输入，第二层共4704个输出。使用如上所示的卷积，我们只需要(5×5×3+1)×6一共456个参数。而如果我们使用全连接层，我们需要多少参数呢？一共3072×4704个参数，多太多了。

卷积网络的参数少，主要是两个原因。

参数共享

每一次卷积的时候，我们的卷积核一直被轮流地使用，输入数据的每一个部分都与过滤器进行了计算。
所谓共享即卷积核的共享。

连接的稀疏性

也很好理解，比如看上图，卷积后结果矩阵的每一个值，都只是原输入数据的一个3*3的数据与过滤器发生计算得到的，不像全连接要关联所有输入值。

更多，也有人说卷积可以捕捉平移不变，即是说一张图片的像素右移或左移了一些像素，它们依然应该有相同的特征。卷积可以给他们打上相同的标签。

总结

这就是卷积神经网络的基本概念，通过tensorflow等软件包你也可以很轻松的实现各种自定义的网络类型。但一般的实际应用中，并不推荐自由构建网络结构，因为卷积网络的训练时间普遍较长，所以当你要建立一个卷积网络来解决一个新的问题时，去尝试想当然的网络结构往往得不偿失。一个好的方法就是多从各大论文或者成功模型的分享中获得灵感，在别人推荐的模型和超参数的基础上构建你的网络，才能事半功倍。

之后会介绍一些经典的卷积网络模型。