Transformer来自Google 2017年的一篇文章，在原来的Attention&RNN模型上抛弃了RNN，用全attention的结构取得了更好的效果。
这里做一做自己学习的笔记，也算一个简单的介绍。
内容图片很多来自于原论文Attention Is All You Need和The Illustrated Transformer这篇文章。

结构

原论文给出的结构如下：

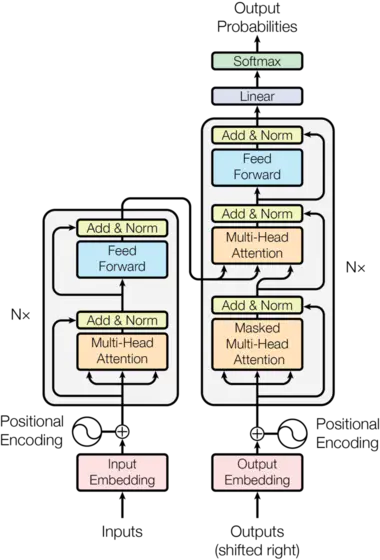
可以看到由左右两个部分，左边的Encoders和右边的Decoders组成。两边都有一个”N×”,表示各自由N个同样的结构重复N次组成，原文中是6。就是下面图中的样子。

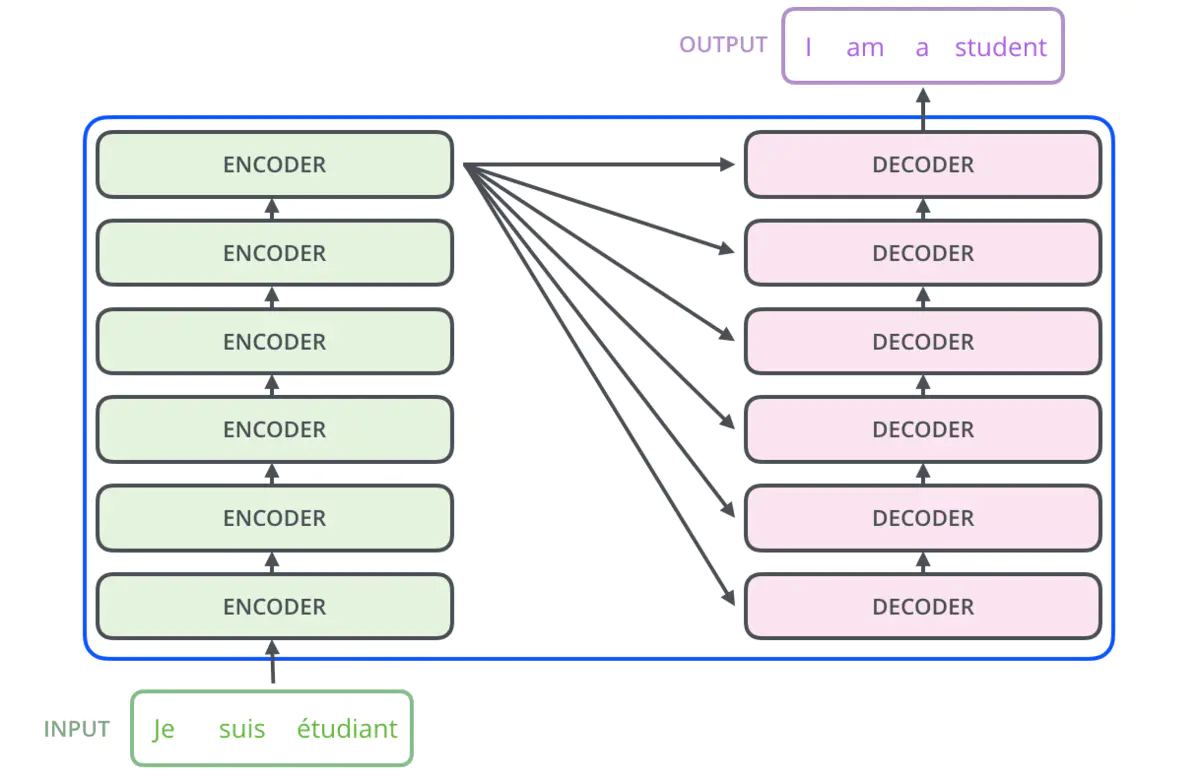
encoder

我们来看一看Encoder部分。

因为是NLP的案例，所以我们首先要把我们的输入数据，即词变成词向量，这通过embedding实现，embedding后的数据作为Encoder的输入。
虽然有很多encoder，但embedding只用在最下面一层的encoder上，其它的encoder都是用上一层encoder的输出作为输入。

每个encoder都是一样的结构，都由两个子结构组成：

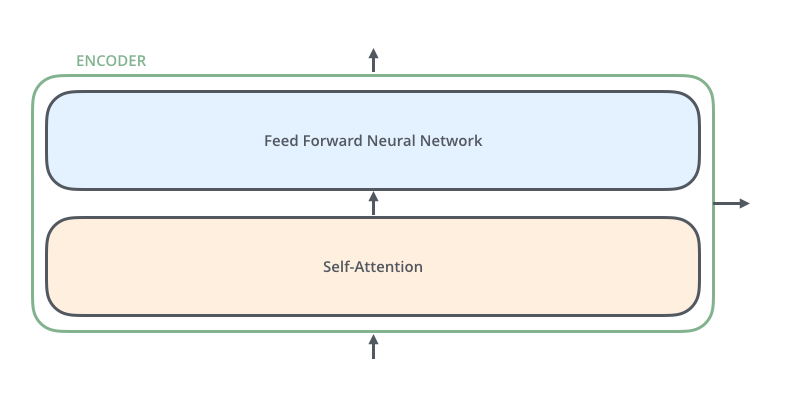
self-attention的作用是，当你在处理某个具体的词时，self-attention允许你从句子中的其它位置处寻找线索，从而对当前词的理解和预测起到帮助。

self-attention 细节

计算self-attention主要有以下几个步骤

第一步
计算self-attention的第一步是从每个输入向量中创建出3个向量(Querry,Key,Value)。他们通过把embedding分别与三个矩阵相乘得到，三个矩阵通过训练过程得到。

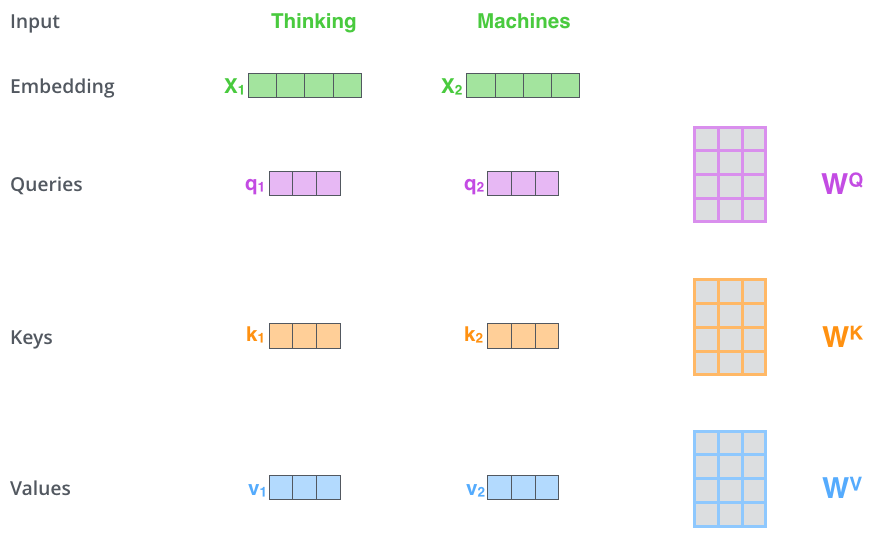
Q,S,V较之embedding的维度要小，在文中的维度是64，而embedding的维度是512。不必完全一样，但这是一种使得计算比较稳定的结构选择。

• Q = WQ * x
• K = WK * x
• V = WV * x

第二步
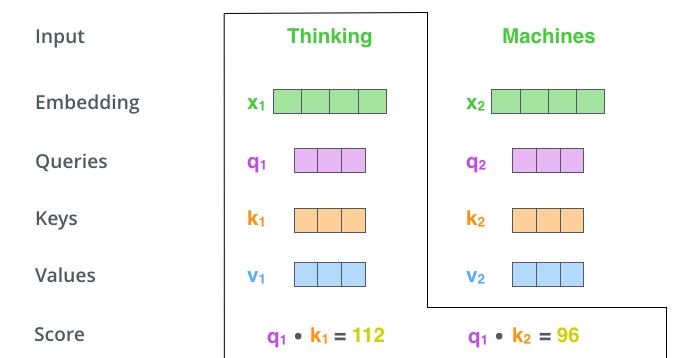
计算self-attention的第二步是计算一个score。 假设我们正在计算的句子的第一个单词为”Thinking”。我们需要把输入的句子中的每一个词与这个词运算来得到一个score，这个score决定了我们在encode当前词的时候句子其它位置所施加的影响。

计算方法是把当前次的Q与要计算的词的K值进行点乘。即如果我们要计算#1位置处的self-attention，第一个我们要计算的score将是把q1和k1点乘，第二个socre则是把q1和k2进行点乘。

第三步和第四步
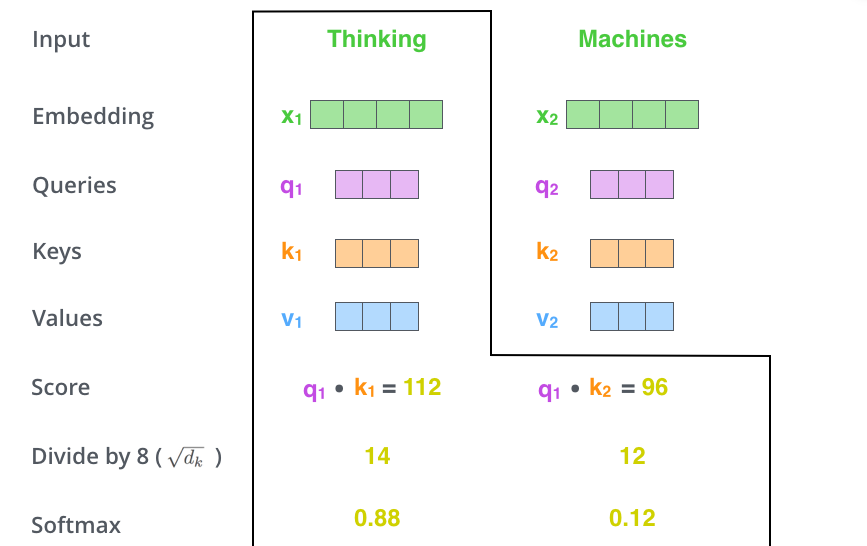
第三步和第四步是将得到的score除以8，这个8是QKV向量的维度64的平方根。这可以让梯度更加稳定(直接归一值差距较大)。当然可以不是8，这里只是一个默认值。接着将结果传递给一个softmax操作，这将把socre的值标准化，使它们都为正，且和为1。

第五步
第五步是将每个V与第四步的结果相乘。这一步从直觉上讲是保留当前词想要关注的其它词语的完整性，同时丢掉不相关的词语(通过乘以了非常小的数)。

第六步
将得到的带权重的数据向量相加。这将得到self-attention层在这个位置(我们这里是第一个词)的输出。

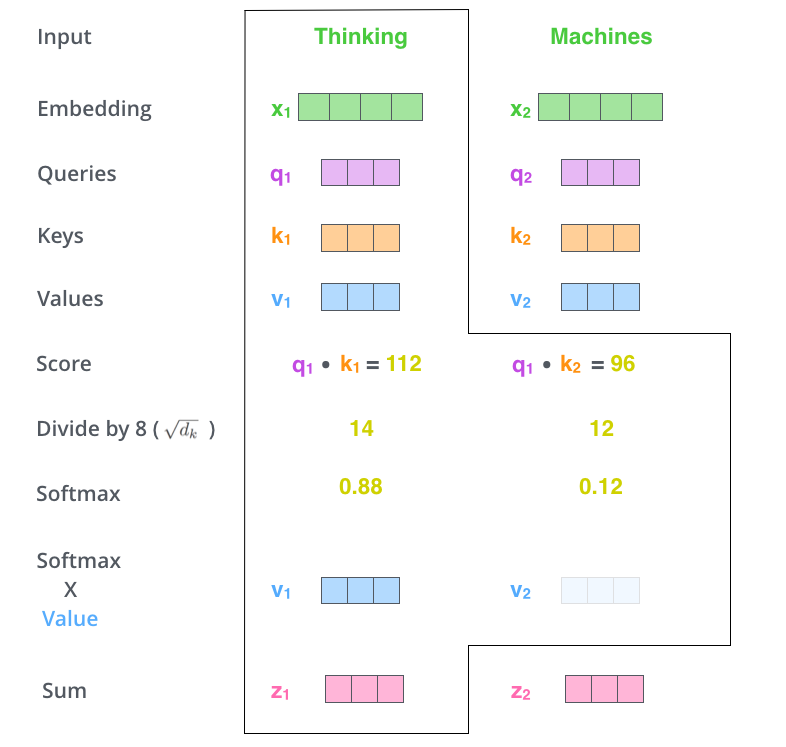
这就是self-attentionde的计算过程，结果向量我们将传递给接下来的 feed-forward nertal network处理。
当然，在实际实现中，这些计算都可以通过矩阵形式的计算从而更加快速。

self-attention的矩阵计算
使用矩阵，第二步到第六步实际上可以在一个公式内进行计算：

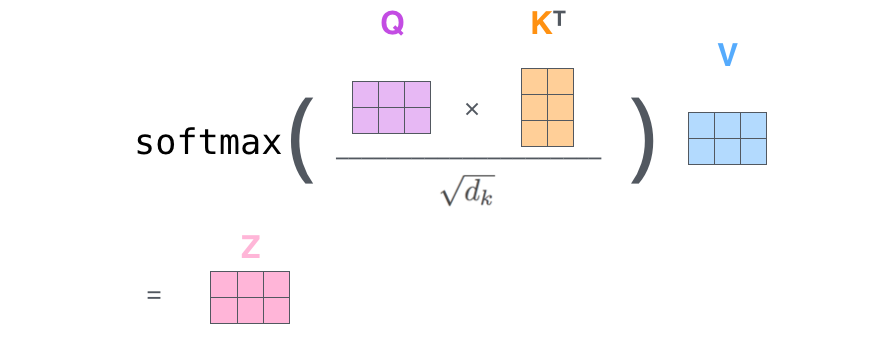
multi-headed

文章进一步用一个叫做”multi-headed” attention的结构增强了self-attention。它从2个方面提升了attention层的表现：
扩张了模型关注其他位置的能力
在我们上面的例子中，对thinking的编码就包含了句中其它位置词的影响(当然，最大的影响依然是它自己)。在解析一些有明显指向性的代词时就显得非常有用。比如“The animal didn’t cross the street because it was too tired”中的”it”指代的谁。
给了attention层多重”表述子空间”
这主要通过多组[WQ,WK,QV]来实现，文中使用了8组WQ,WK,QV，这些矩阵都通过随机初始化赋值。即是说我们会得到8组QKV，从而得到8个输出矩阵。每一个都是输入数据的一个表述子空间。

在传递给feed-forward network前，我们需要将他们处理成一个矩阵。通过将这8个矩阵堆叠起来，再与一个权重矩阵WO相乘得到。

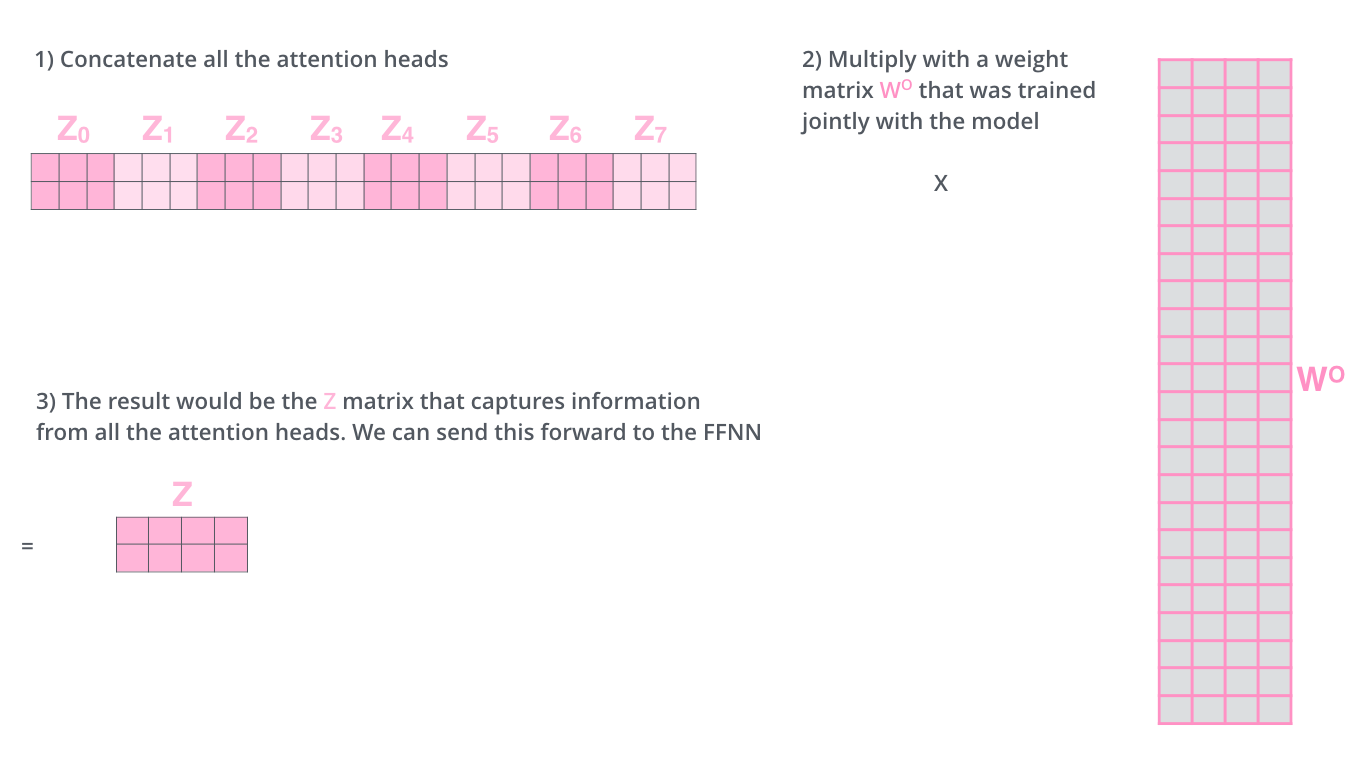
以上大概就是 multi-headed self-attention 的内容。原文将他们放到一张图上：

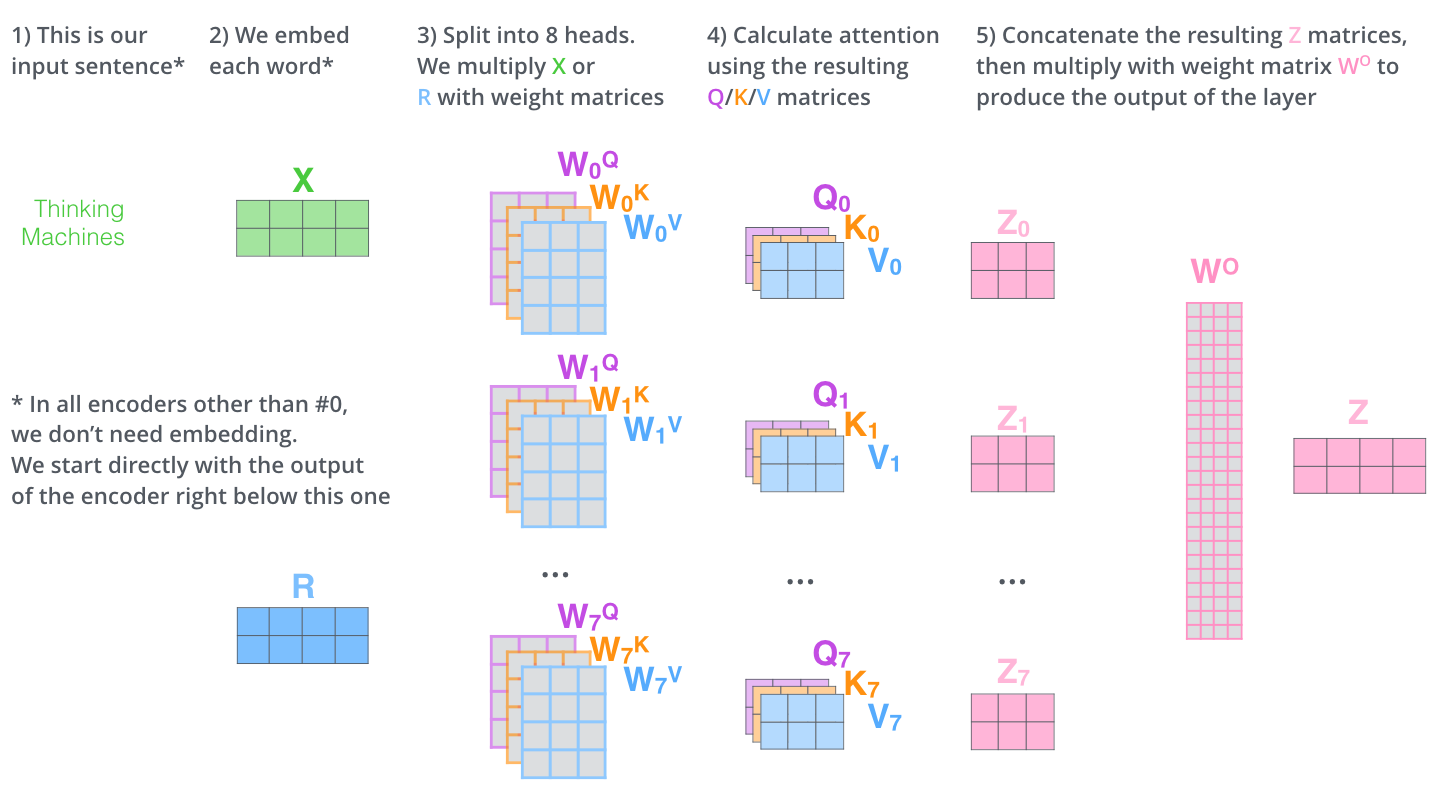
position encoding

因为放弃了使用RNN，那么句子中词与词的位置关系就被忽略了，文中使用了一种position encoding的方式将位置信息补入模型中。
这通过给每一个input embedding加上一个vector来实现。这些vector遵循一种特殊的模式，它存储了每个词的位置信息，通过把它与embedding相加，从而把这种信息代入到后面的QKV和点乘的计算过程中。

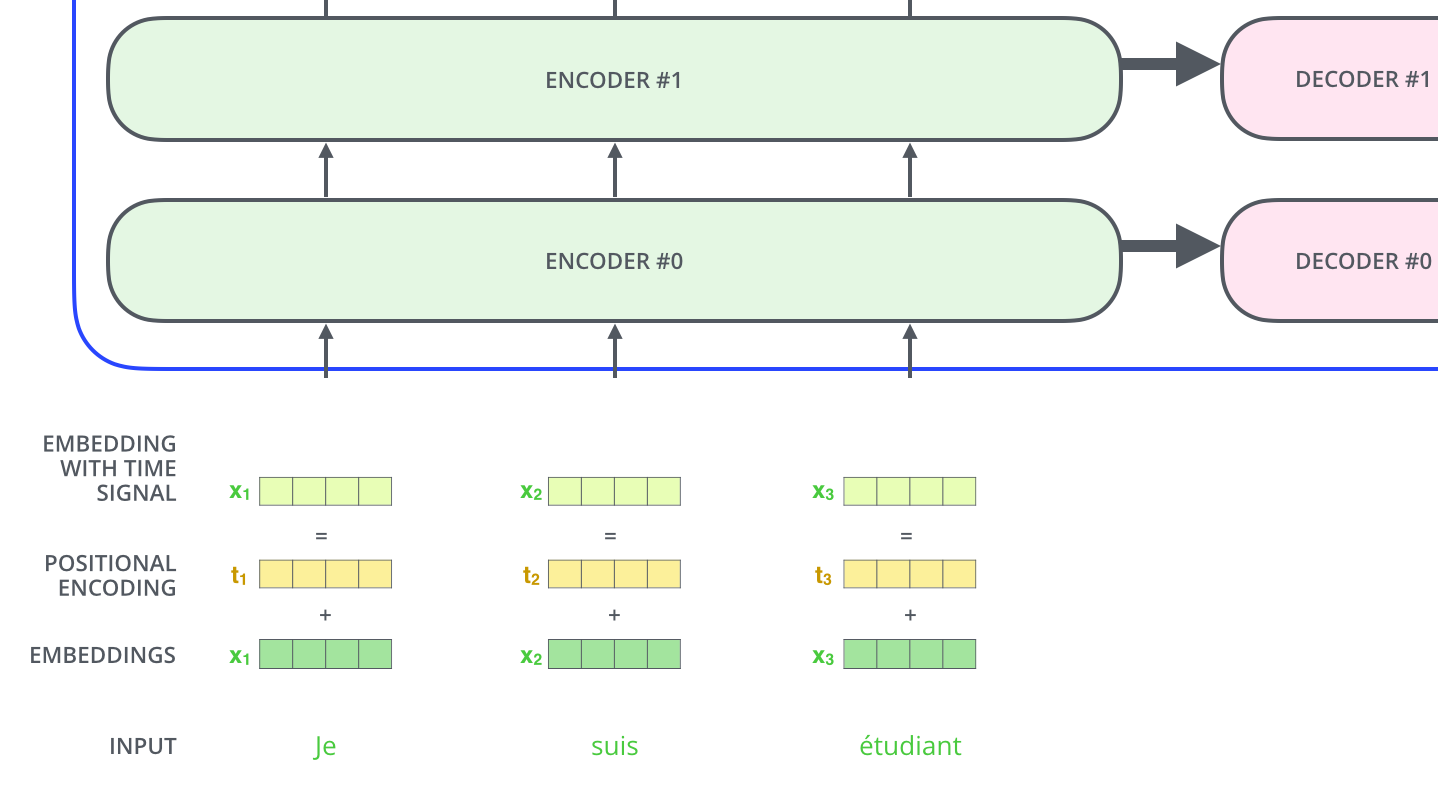
如果我们的embedding是512维的向量，那么要加的positional encoding 向量也是512维。

关于位置编码，文中使用的是三角函数的形式。

大概说一下什么是位置编码和为什么要使用三角函数。
要对位置进行编码，最简单的方式莫过于直接使用单词在文本中的位置，即1，2，3，…，N。但缺点过于明显，如果文本较长，那么位置编码的大小跨度就太大了，将这样的数据加入到模型训练中，很有可能是会喧宾夺主的抢占embedding的重要性。
同样，将刚才的顺序除以文本长度也是不行的，如1/N,2/N,3/N,…1。
我们需要位置信息，其中一个重要的信息就是相对位置信息，而这种处理方式，会导致相隔同样距离的两个词，在长度不同的文本中得到的相对位置信息不一致，甚至差距较大。
总结之后，那么真正适合用来做位置编码的函数似乎就是 连续且有界的周期性函数。有界保证值域不会太大，周期性保证一定程度上编码的差异会摆脱文本长度的影响，而连续则保证了两个比较靠近的词不会出现差距很大的情况。

于是文中使用了sin和cos函数，连续而且周期稳定，值域[-1,1]。

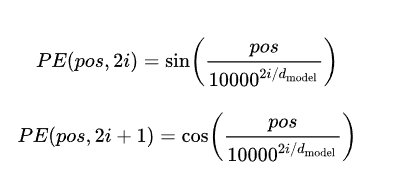
加入了dmodel和i两个参数，dmodel是embedding的维度，在文中就是512，用于增大位置编码的空间表现范围。i为向量的某一维度，dmodel=512，那么i就是[0,255],这样在奇偶维度分别使用sin和cos。这样就从取值范围和取值方法两个方向上增加了取值的多样性。让位置编码更加科学。

当然，这个函数作者应该也是通过自身的经验与不断的实验得到的。

PS：GOOGLE BERT中用了新的取位置信息的方法，position embedding，这是后话。

残差网络(Residual network)的使用

另一个细节，就是哪里跑不掉的resNet的使用：

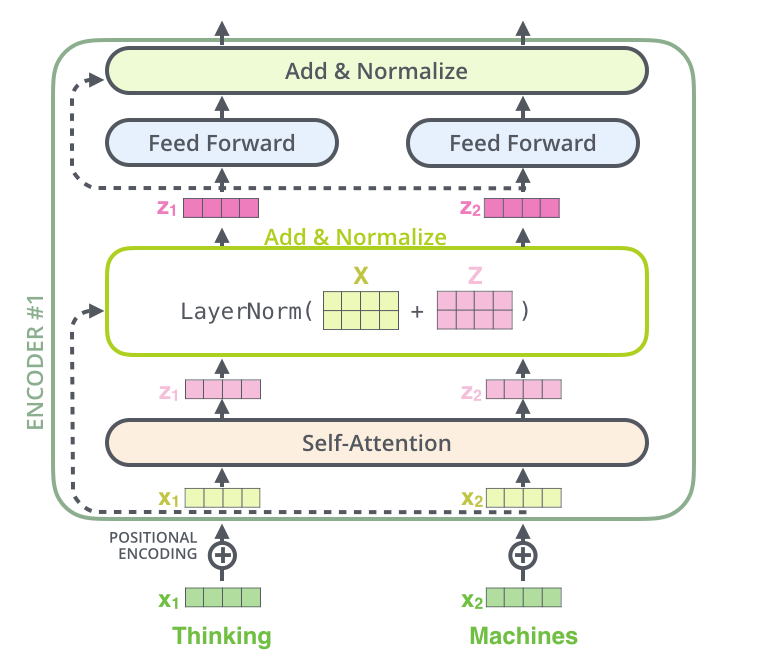
同样，在decoder中也使用到了resNet，如果是一个2个encoder和decoder的transformer，它长这样：

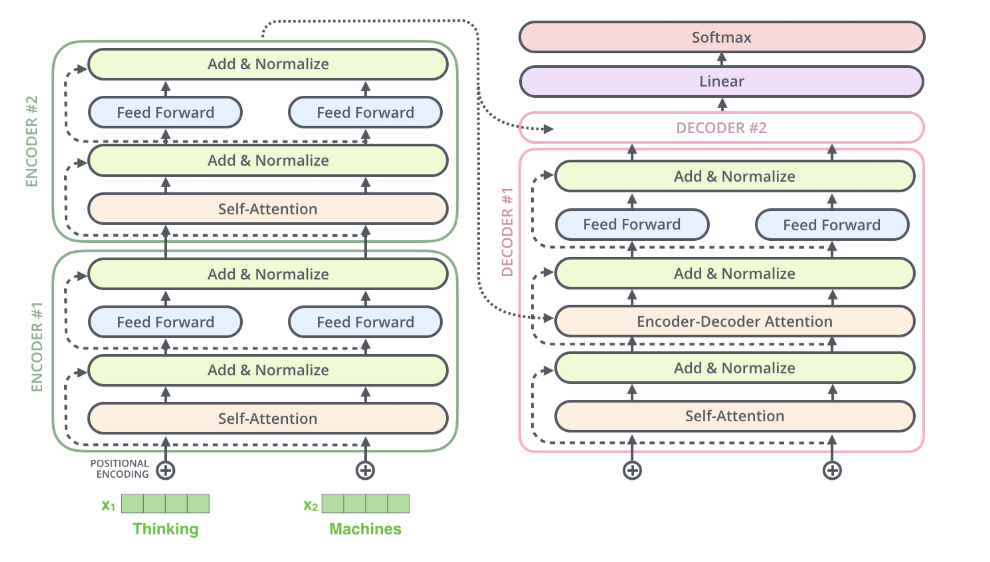
Decoder

介绍完Encoder，大多数Decoder里的组件的作用也明朗了。接下来看看他哥俩如何一起工作。

再贴一下模型结构图：

可以看到Decoder中有一个 Encoder-Decoder Attention 层，它接受Encoder部分最后的输出作为计算attention的Key和Value，接受它下面的self-attention层的输出作为Query。

其次，Decoder部分的self-attention层也与Encoder中的不同，不同于Encoder中计算单词两两间的attention，Decoder中计算的是当前单词和它前面的单词的attention，同样，也要加入位置信息。

文章中有张非常形象的动图：

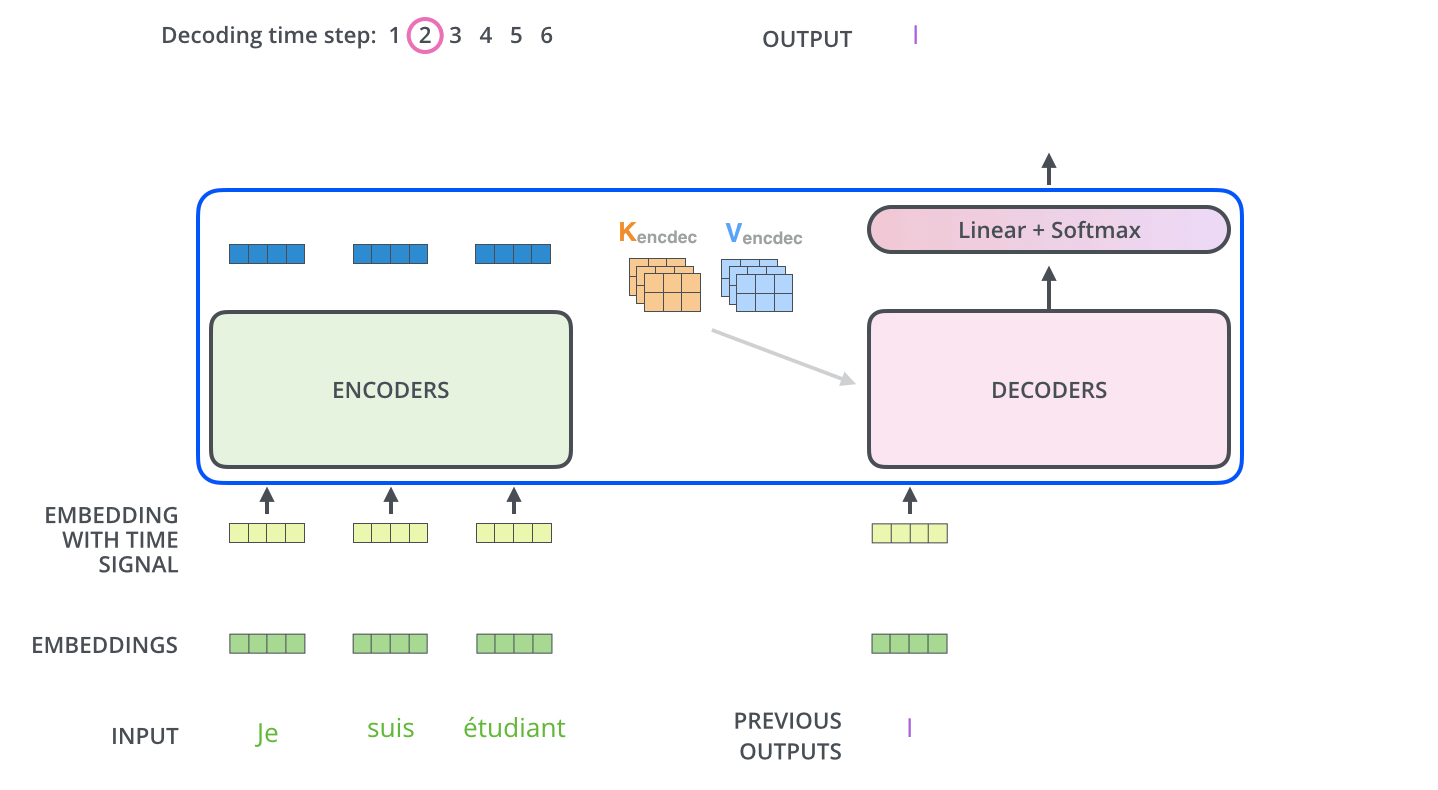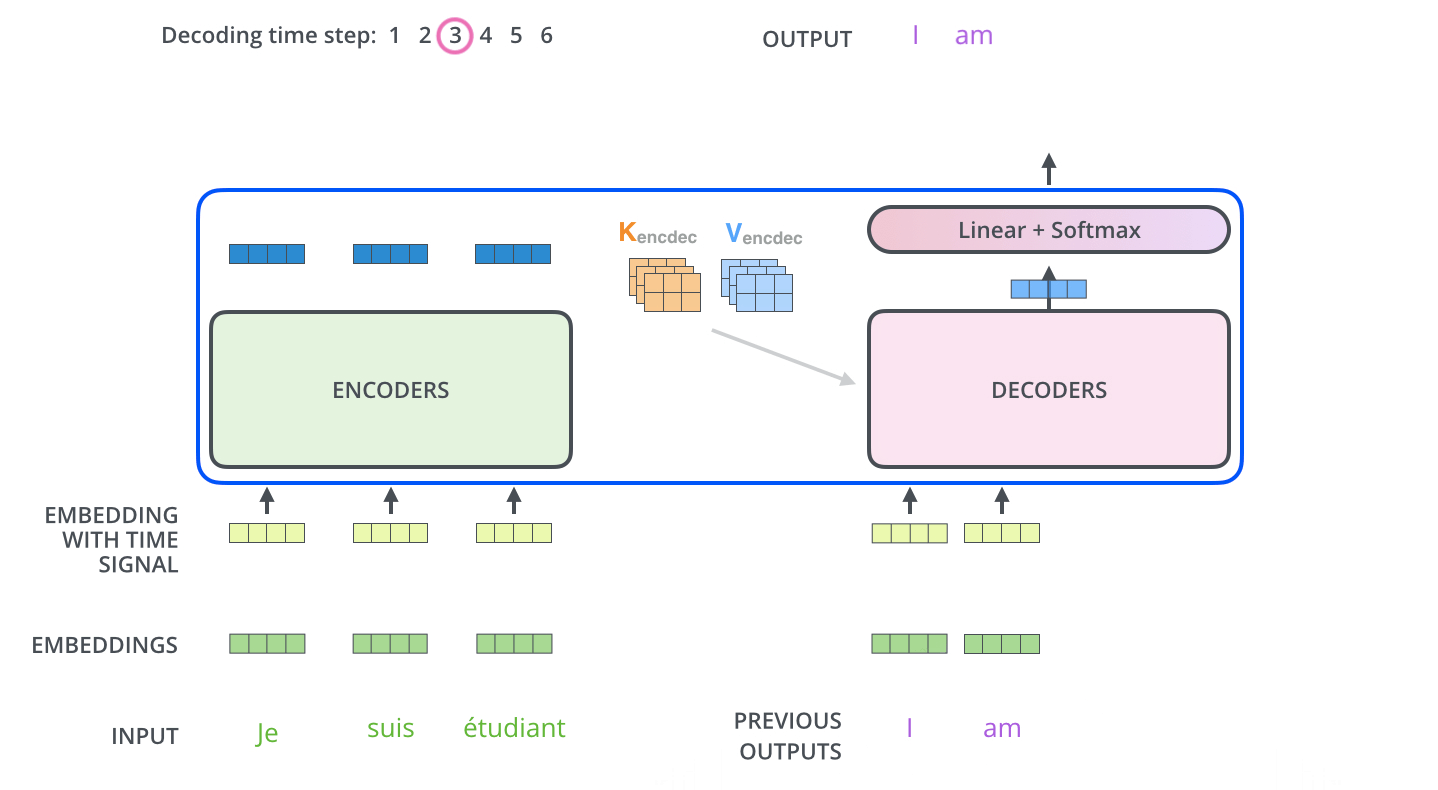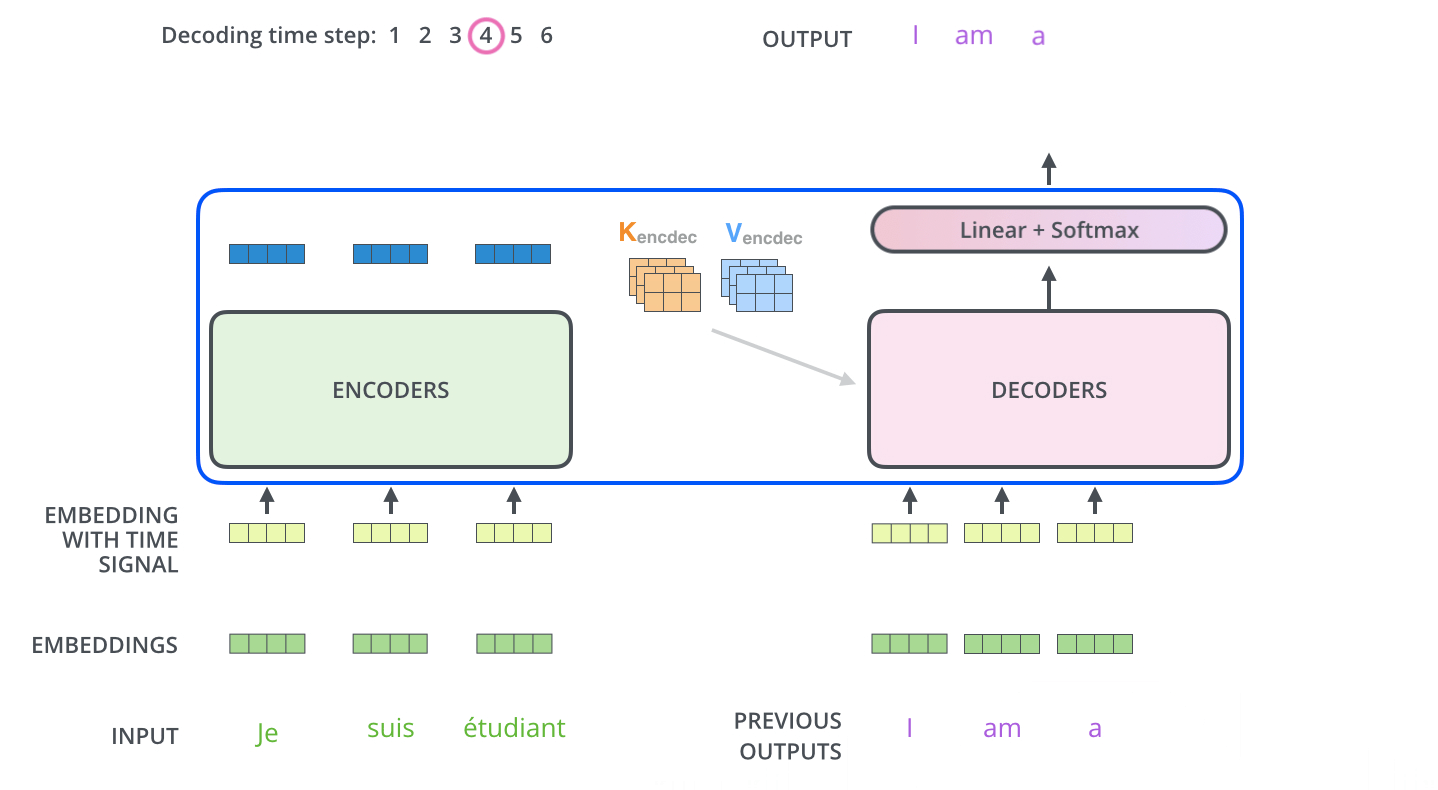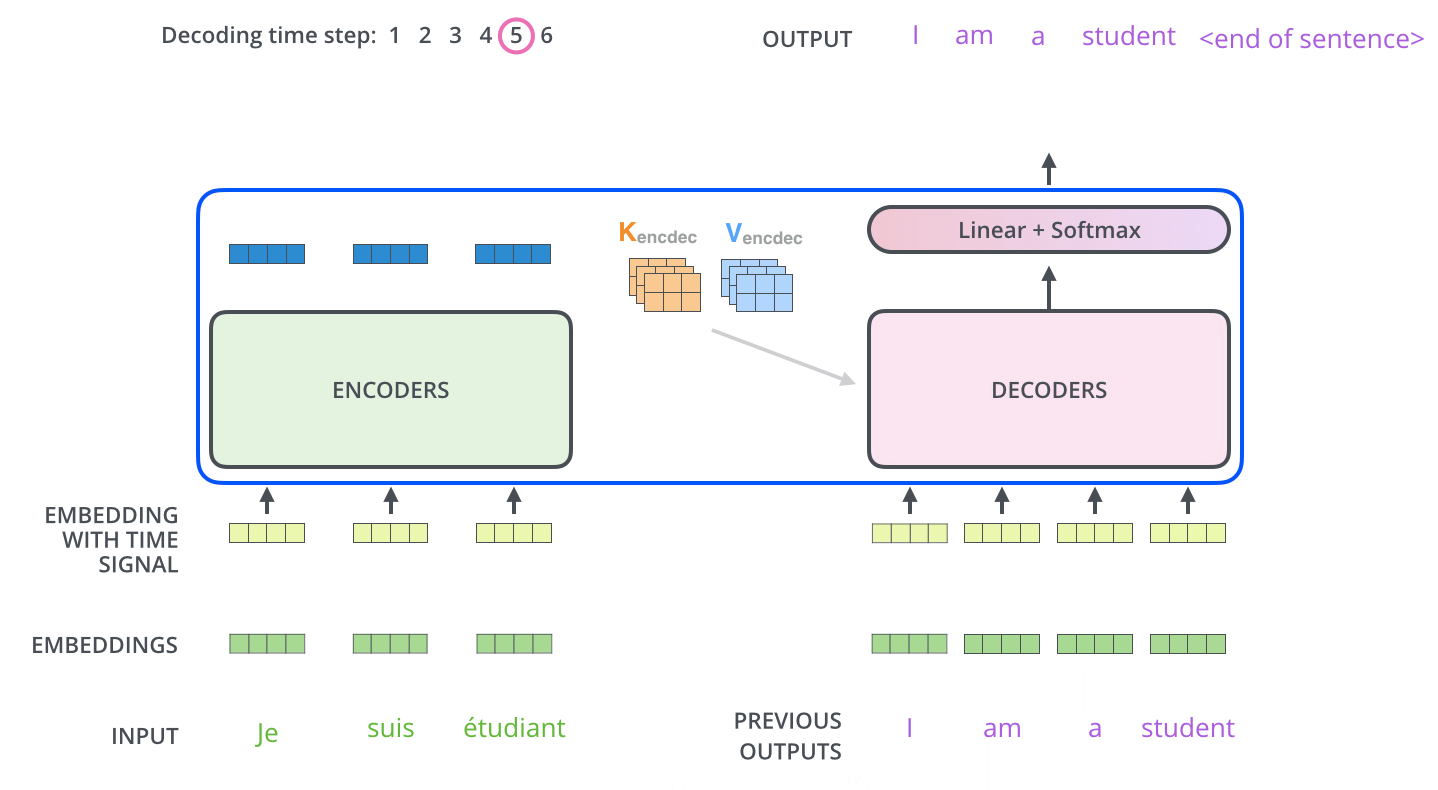
注意在decoder中做self-attention的时候，当前输入只应该看到当前时刻以前的输出，比如在输出第二个词的时候，输入中是不应该出现第三个词的信息的。文中处理这种情况的方法是用了一个倒三角矩阵(第i行j列的元素表示第i个输入和第j个输入的attention)，将对角线右侧元素全部设置为负无穷，这样就防止了模型看到未来的信息。

最后一层

decoder将输出一堆floats组成的向量，将它转换成词语，就是最后一层的工作(通常是一个Linear+Softmax)。

Linear layer是一个简单的全连接层，将decoder的输出投射为一个比原来大很多的向量，叫做logits vector。

如果我们的词空间有10000个单词，那么10000就是这个logits vector的维度，向量中每个元素对应一个具体的词。接下来你就清楚了，softmax的作用是将这个logits vector的结果变成概率，概率最高的元素对应的词就是我们的输出。

关于训练

todo…

代码

todo…

参考

The Illustrated Transformer
Attention Is All You Need
哈佛大学的pytorch版本源码