深度学习中的优化器有很多种,除了我们熟悉的梯度下降外,还有一些诸如 RMSProp,adam 等优秀的优化器。来了解一波~
梯度下降 GD,BGD,MBGD
梯度下降(GD:gradient descent)大家都很熟悉,这里也不做详细介绍。整体就是先初始化求解参数,然后通过求解损失函数对求解参数的导数来对我们的求解参数进行更新,直到收敛。
梯度下降分为BGD(batch:批量梯度下降),SGD(stochastic:随机梯度下降)和 MBGD(Mini-Batch:小批量梯度下降),区别在于每次更新梯度时使用的样本的数量,分别为全部样本,单个样本和一部分样本。
梯度下降找到的最优解一般为函数的一个鞍点,即局部最优解。
MBGD和SGD因为样本较少,随机性太强,梯度往往震荡很大,如下:
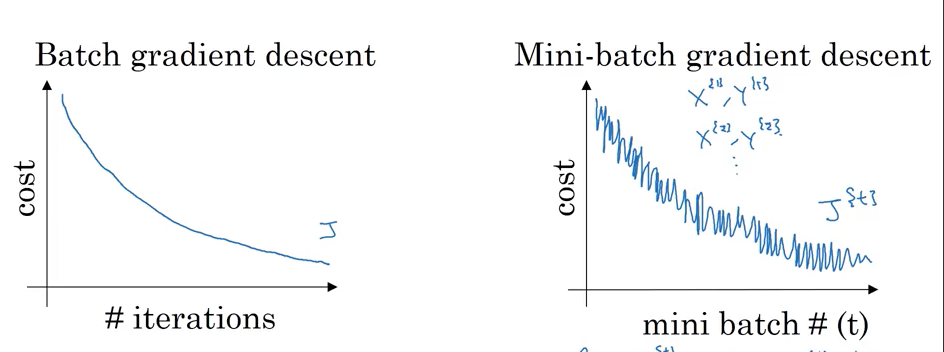
要解决这个问题,使用MBGD进行优化时我们可以对学习率进行衰减来使之收敛。
PS:因为计算机本身的一些性质,将批次量设置为2的幂数计算会更快。
当然,还有比小批次下降更快的算法。但在学习它们之前,我们首先要了解指数加权平均。
指数加权平均
什么是指数加权平均?
参考吴恩达老师对此的讲解,用一个例子来进行说明:
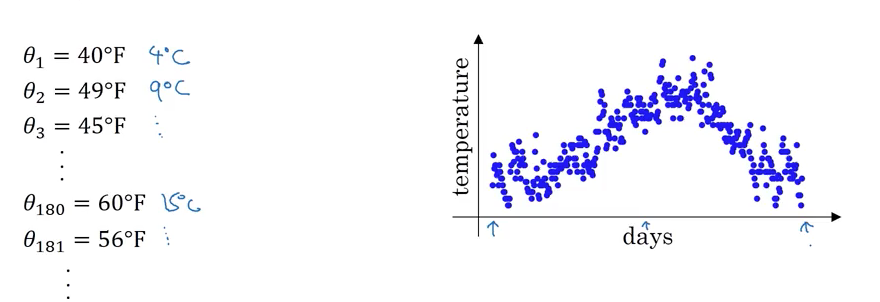
上图是伦敦一年之中每天的温度情况,我们来对它做一些处理,把每天的温度值记作Vn。则:
V0=0, V1 = 0.9*V0 + 0.1*θ1, V2=0.9V1 + 0.1*θ2,…
θ为上图中当天真实的温度值,这个0.9我们记作β,那么公式记为:
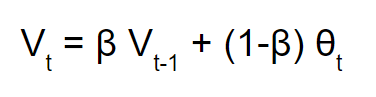
稍微进行一下联想,这个V可以近似看做是之前1/(1-β)天的平均值,当我们分别取β=0.9(红色曲线)和0.98(绿色曲线)时,图像为:
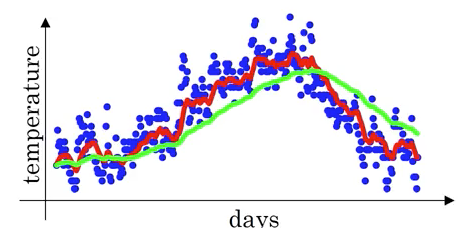
β取0.9,我们把这个式子展开:
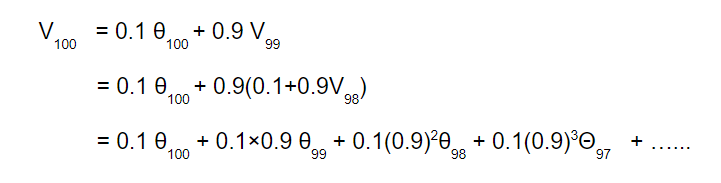
θ随着时间推后是β的指数级衰减,且一般来说,指数加权的衰减大约会在1/(1-β)后衰减到大约三分之一的程度,比如0.9的1/(1-0.9)次方约等于0.35,所以我们说它大约是最近10天的平均值。这就是指数加权平均名称的由来。
指数加权平均减少了存储空间的使用,当我们需要某个V的值时,只需要通过计算即可获得,因此它在机器学习中得到了大量的应用。
细心的你可能注意到,我们的V0取值为0,这会在计算初期的时候产生较大的误差值。
因此在很多时候,我们会对V的值进行偏差修正。
使 Vt = Vt/(1-β^t) ,从而对Vt进行放大,而随着t的增大,放大率会逐渐趋于1。
有了这个基础,我们就可以介绍一些其它的优化器方法。
动量梯度算法(momentum)
算法的主要思想其实很简单,就是把我们刚才学习的指数加权平均用来计算梯度,然后用计算得到的梯度来进行参数更新。
在上面的梯度下降算法中,考虑多维度的情况,如下:
于收敛来说,竖直方向的震荡显然是无益的,我们希望能够减小竖直方向的震荡。
动量梯度下降的步骤如下
第t次迭代:
- 用当前小批量样本 计算 参数W和 偏差b的导数
- Vdw = βVdw + (1-β)dw, Vdb = βVdb + (1-β)db
- W := W - αVdw, b := b-αVdb
end
我们还是对批次数量进行迭代,整个算法中中有2个超参数,α和β,α为学习率,β是我们上面学习到的指数加权。
为什么咋这么做可以有效呢?因为指数加权平均的平均,它就让垂直方向上相反的震荡被平均从而变小,而水平方向的震荡方向是相同的,平均值依然很大,故整体收敛速度就加快了。
PS:动量梯度下降时基本不用偏差修正,β基本都是选择0.9。
RMSprop
RMSprop全称为均方根传递(Root Mean Square prop), 它也可以加速梯度下降。
计算方式如下:


RMSprop主要的思想是缩小大的震荡,加快小的震荡。如上图,垂直方向的震荡很大,而水平方向很小,RMSprop就会缩小垂直方向的震荡,加快水平方向的速度。
原理很简单,如果垂直方向的震荡较大,那么Sdb就会很大,那么作为除数,更新速度就减慢了,相反,水平方向较慢,Sdw就较小,W的更新速度就加快了。
当然,实际应用中,并没有垂直水平这么简单,我们加快的是慢的维度,减慢的是快的维度。
而且为了防止除0发生,通常在分母上我们会加一个很小的EPSON,大概10e-8
接下来,我们把RMSprop和动量结合起来,会得到一个更好的优化算法。
为了防止冲突,RMSprop中的β,我们用β_2表示
Adam
adaptive moment estimation 自适应矩估计
adam优化算法实际上就是将RMSprop和动量梯度下降结合起来的算法。
在机器学习领域和深度学习领域中,曾经提出了非常多的优化算法,但大多数算法都不能很好的适应于不同的网络结构,adam算法是少有的在非常多网络结构中都能够产生非常好效果的算法。
在机器学习领域和深度学习领域中,曾经提出了非常多的优化算法,比如Adagrad,Adadelta等,但大多数算法都不能很好的适应于不同的网络结构,adam算法是少有的在非常多网络结构中都能够产生非常好效果的算法。
初始化Vdw,Sdw, Vdb, Sdb为0

l为网络层数,两个β分别是动量梯度和RMSprop中的加权,α为学习率,同样,为了防止除0发生,通常在分母上我们会加一个很小的EPSON,大概10e-8(上图没加)。
几个超参数,一般β1选择0.9,β2选择0.999,EPSON选择10e-8。
而α,一个好的方法就是逐渐减小学习速率,使用一个衰减率来对学习率进行衰减。
本博客所有文章除特别声明外,均采用 CC BY-SA 3.0协议 。转载请注明出处!