引子

最近在一边写一个web qa的问答模型一边刷leetcode，前者踩坑太多耗费了超出我预期的时间(还是攻城能力欠缺啊- -)，于是文章也有一段时间没更新了。
这期间抽空回顾和学习了目前工业界推荐系统常用的架构和算法，也亲自用代码实现了其中的部分算法，但总体还是停留在纸上谈兵的阶段。
虽然这篇文章我脸很厚的用了“概览”这个词，但我们都知道真实的工程落地远比纯粹的算法来得复杂，除了对应实际问题的难度，还会遭遇很多预想不到的困难，当然，这是题外话了~

这篇文章基本是对我近期看的这些推荐系统算法文章和视频的一个个人的文字总结，希望自己之后有应用的机会吧~

相关链接会放在文末。

概述

工业界推荐系统的架构基本在宏观上比较趋同，大都可以粗分为召回(recall)和排序(rank)两个阶段。如下：

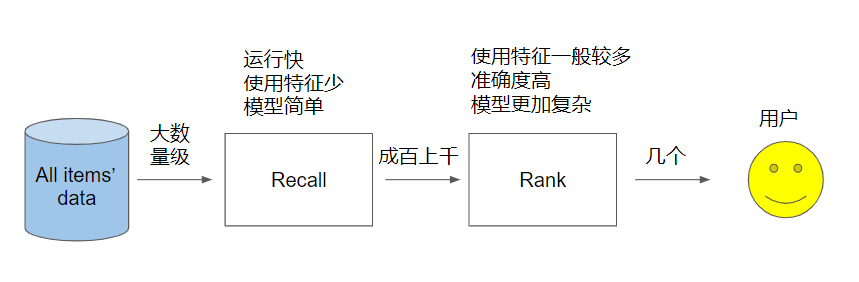
一般来说，平台往往动辄有上百万的item，不管是新闻应用，视频应用还是电商应用，要从海量的item中直接一步到位准确地找到推荐给某个用户的item是比较难的。 这两个阶段可以大概地看成是粗筛和精选，对某个用户来说，先通过一个比较快速而简单的方法从上百万的item中筛选出几百或者几千个高质量的item，再通过一个精确的方法仔细地将其中最好的一些item优先级确定下来，然后推荐给用户。前者就叫做召回阶段，后者则叫做排序阶段。

当然，落地的时候往往还会把排序阶段再分成 粗排-主排-重排，于是变成了四个阶段，这个后面再说~

下面就来介绍一下各个阶段常用的算法。

召回算法

召回算法有很多，主要分为3类：

• 基于用户行为，简单地说就是“你看了什么，我就给你推荐什么“
• 基于用户档案，即给用户建立档案，根据用户档案中的标签推荐相应的item
• 基于隐语义，即基于机器学习方法，使用类似于embedding的方式
  三者各有特点和优劣，基于用户行为直观上显得过于简单，基于用户档案也会存在用户改口味难以泛化的情况，而机器学习，本身就偏向黑盒，对于算法中的中间值难以解释，从而优化和修改显得困难。

所以在使用这些算法的时候，一般是使用多路召回，即使用很多不同的召回算法分别进行召回，再把各自召回的结果组合起来作为最后的召回结果。

这里主要介绍 CF, personal rank, item2vec等算法。

CF(协同过滤)

协同过滤是一种很老的算法，但沿用至今，它能够实现对特征进行学习的算法，即能够自行学习所需要使用的特征。

算法的核心是通过学习得到2个维度较低的矩阵，一个代表用户的embedding矩阵，一个代表item的embedding矩阵，计算某个用户对于item的推荐值的时候，只需要将二者进行点积计算。再直白一点，比如电影拥有两个特征，动作属性和爱情属性，某用户A的embedding向量为θ=[5，1]，即A对电影中动作元素的偏爱为5，相对地对爱情元素的偏爱只有1。而某一部电影的X=embedding为[4，1]，那么我们将这2个向量直接进行点积，matmul(θ,transpose(X))，得到的值就是这部电影对于这个用户的推荐值，将不同电影的推荐值进行排序，其中推荐值最高的不就是应该推荐给A的电影了吗。

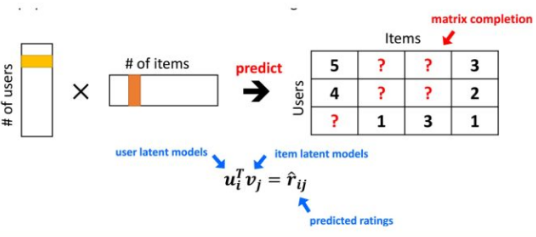
怎么得到这两个embedding矩阵呢？基于上面电影推荐的例子，假设我们知道每部电影的特征矩阵，即X已知 求θ。那这个问题就变成了一个很简单的线性回归问题。 已有的打分数据作为样本，我们的目标函数只需要将 θ·XT减去真实评分 作为误差，很简单就可以定义出目标函数：

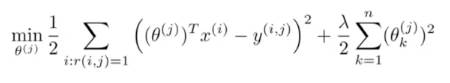
其中

• θ^(j)代表用户j的embedding向量。
• x^(i)则代表电影i的embedding向量。
• r(i,j)为1表示用户j已经为电影i打了分，0则表示没有。
• y^(i,j)为用户j给电影i的评分
  将这个公式推广到所有用户：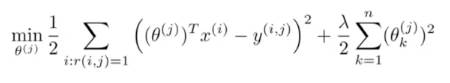

有了目标函数我们在将其对θ求导

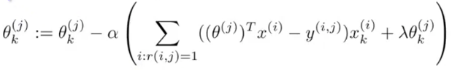
然后直接用梯度下降之类的优化算法进行求解即可。

同理，假设θ已知，我们也可以用同样的方式求得X。

你可能会想，这不就成了鸡生蛋还是蛋生鸡的问题了吗？问题是两者我们都不知道啊？

是的，你很清醒，没有被带偏，实际情况中，用户的偏好和电影的属性都很难收集，更别提特征这个东西本就虚无缥缈，爱情属性动作属性你还能够理解，真出来几百个特征，你能分清什么是什么吗?

这个时候协同过滤就钻出来了，在面对这种两个未知数可以互相更新的情况下，最好的方式就是初始化其中一个未知数，然后求得另一个未知数，再反过来求第一个未知数，以此类推，在这个过程中，2个未知数就会产生协同作用，终会完成收敛，达到生命的大和谐。想想pagerank,想想EM，是不是很熟悉~

除了让二者彼此更新，还可以将二者同时计算：

第一个式子是对每个用户，通过他们评价过的电影的类别来推断用户的喜好。第二个式子反过来，对每个电影，找出评价过它的用户的喜好来推断电影的类别。

其实二者前半部分就是第三个式子中的第一部分，只是第三个式子取得是一个(i,j)的对，表示所有用户评分过的电影。然后把二者的正则化都加上。实际上关于第三个式子，假如你假设x为常数，它就等于第一个式子，你假设θ为常数，它就等于第二个式子。

这就是协同过滤，实际实现过程中是可以用向量化实现从而不需要一个一个地进行计算的。这样的实现也叫做低秩矩阵分解(low rank matrix factorization)，还有一些地方叫做LFM(latent factor model)。不过矩阵分解方法并不是只此一家，SVD也是其中的佼佼者。这些方法最终都是得到user-item的隐式矩阵分解，获取二者的隐相量。

personal rank

推荐系统中最基础的两个部分就是user和item，整个系统也是user和item的交互，很容易想到，这就是一个图结构。那么，聪明的先行者们就想，能不能使用图算法来进行个性化推荐呢？ 当然可以~

user和item构成的图是一个二分图。

摘抄一下百度百科二分图的解释：
二分图又称作二部图，是图论中的一种特殊模型。 设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边（i，j）所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B)，则称图G为一个二分图。

而对于推荐系统而言，用户和item刚好是一个二分图，顶点分为user和item两类，且所有的变都是连接一个user和一个item的。

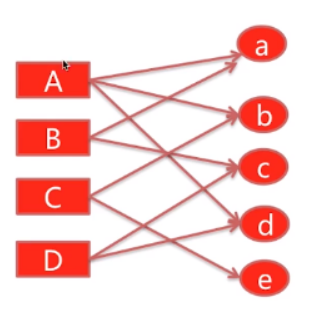
如上user和item构成了一个二分图，大写ABCD表示user，小写表示item。
personal rank比较各个item对于某个user的推荐值基于以下规则，其重要性一次递减：

1. 两个顶点间有多少条路径可以连通，如上图，从A-c，有A-a-B-c, A-d-D-c两条，而从A-e只有A-b-C-e一条，则c更值得推荐。
2. 如果第一条相同，则比较连同路径的总长度，长度短者更值得推荐
3. 如果1，2相同，则比较连同路径经过的顶点的出度和。

基于此规则，我们来介绍personal rank方法的详细操作：
将二分图视作无向图，对于用户A进行推荐时，我们就从A节点出发开始在图上进行随机游走，以概率α从A所有的出度中等概率选择一条前进，到达对应顶点后(比如到了b)，再次以α的概率继续从a的出度中 等概率地选择一条继续前进，或者(1-α)的概率回到起点A，经历很多步之后，统计A到达各个item节点的次数求得概率。可以证明，只要步数足够大，此概率可以收敛。

把固定item对固定user的推荐得分记作PR值

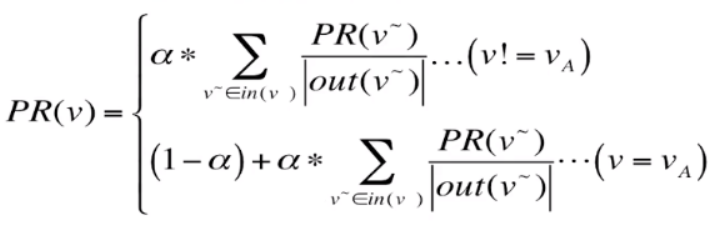
其中out(v~)表示节点的出度。

可以看出，和pagerank算法非常相似，某个点的PR值等于 可以连通到该点的其它点的PR值除以自身出度 的和，即如a，有A,B可以连接到它，而A出度为3，B出度为2，故PR(a) = PR(A)/3 + PR(B)/2，再乘以一个概率α。A自身的PR值还要加上一个(1-alpha)。

直接迭代计算，复杂度太高了，像pagerank一样，我们也可以祭出矩阵来做：

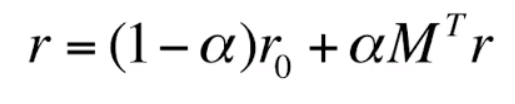
• r是一个n维向量，n是图中所有的节点数量，包括user节点和item节点，值则是每个节点的PR值。
• r0也是一个n维向量，只有对应出发节点的元素为1，其余节点为0。
• M是一个n阶转移矩阵，即图中节点与节点之间转移的概率，很好理解。 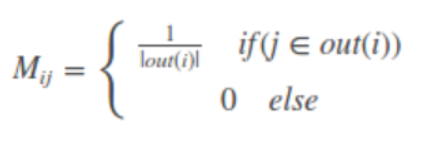这样不断将结果代入公式，r最终可以收敛。

再对公式进行移项处理，得到：

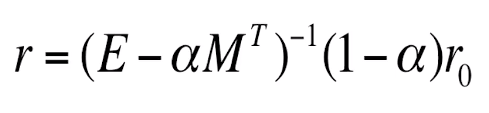
向量化实现很简单，你把r0换成矩阵试试。

PS：

• 在计算时很多喜欢去掉1-α这个值，是因为推荐时我们更多的是要的推荐排序结果，而不是具体的推荐值，故去掉一个常数乘子没有影响。
• 可以看到其中M是稀疏矩阵，故E-αMT也是稀疏矩阵。针对它的存储和计算都有很多成熟的方法。

item2vec

item2vec是一个神经网络算法，它基本是属于word2vec的衍生品。word2vec算法在诞生后，其简洁的方法和出色的效果掀起了一股万物皆可embedding的热潮，item2vec就是将word2vec应用到推荐系统上的算法。

所以要说item2vec，就逃不了word2vec，word2vec是一个用于NLP的算法，由大神Tomas Mikolov在2013年的论文《Efficient estimation of word representations in vector space》中提出。word2vec是一篇跨时代的论文，在word2vec诞生前，语言中的词都是使用one-hot、tf-inf等统计学方法或者NNLM这种计算量非常大的n-gram方式进行表示的，这样就会使得数据维度特别高(语料库大小)和精度低，而且词与词的关系也被忽略了。word2vec是一种将其进行降维，并且可以表示出词与词关系的方法。而且从它开始的embedding的概念，使我们在NLP研究方面，也终于可以开始站在巨人的肩膀上了。

它使用的方式就是embedding，将词用向量来表示。如下：

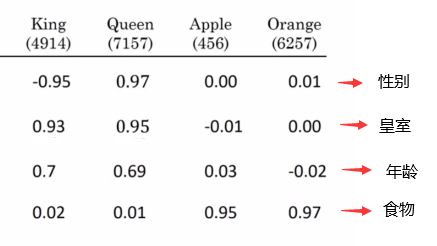
每一列是一个词的向量表示，向量中的每个值可以看做是一个特征，比如king和queen在性别和皇室上都非常突出，这是非常符合直觉的。
注意：上图只是为了举例，真实的embedding向量中的值基本是很难解释的。

要得到词的embedding,我们只需要将embedding矩阵与该词的one-hot相乘，如下：

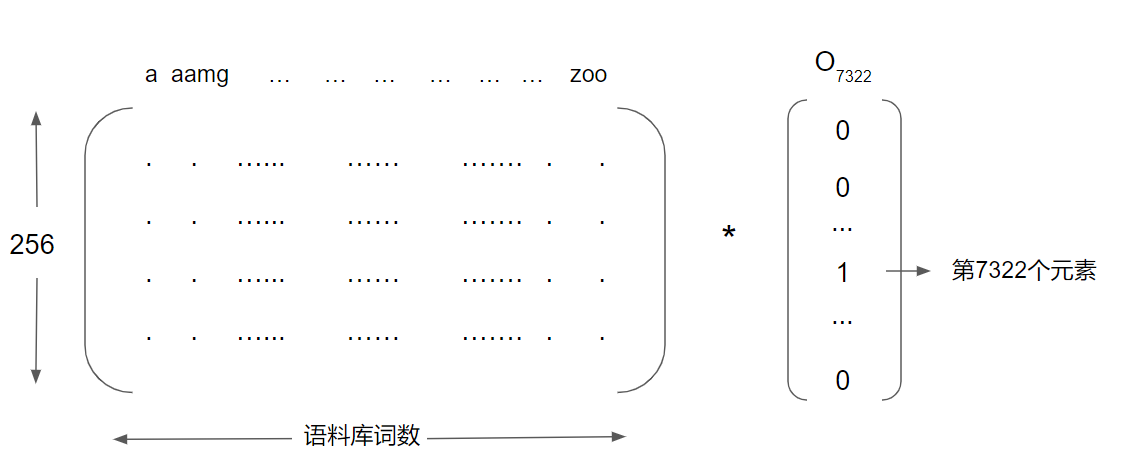
这个embedding矩阵如何得到呢？

word2vec论文中介绍了2种方式，CBOW和skip gram。我以skip gram为例作一个简要的介绍：

比如我们的语料库大小为10000，现在有一个英文句子： I will try to climb a very high mountain tomorrow.
我们随机选择其中一个词来预测它上下文的其它词，比如 climb，接着我们就可以在它一定的上下文范围内选取词作为样本，如：(climb,mountain),(climb, high),(climb, I),(climb,to)。

接着我们使用这些选取的词的one-hot来乘以一个Embedding矩阵 E得到其词向量，再通过一层神经网络+softmax得到一个10000维的向量，向量的各个值就代表每个词出现在其上下文中的概率。
即： Oc * E = ec -> θT * ec -> softmax -> yhat
其中E和θ就是我们的待训练参数，直接使用优化器进行更新，便可以得到我们的E。

而CBOW则差不多，区别在于CBOW是用多个词来预测一个词。

当然，word2vec还有很多的细节，比如如何通过分层计算或者负采样来减少softmax层的计算量以及选取上下文词的启发式方法等。你可以在文末找到该论文进行翻阅。

而item2vec 就是把item当作词，一起出现的item当作上下文(比如用户浏览的item的集合)，使用上面的word2vec方式学习到item的embedding矩阵，有了它，再用任何向量近似算法计算向量相似性作为item相似性还不是任你施为~

比如根据用户最近浏览过的item推荐与之相似的item。

和CF的区别
都是计算隐相量embedding，item2vec和上面介绍的MF主要的区别就是MF计算的embedding是user-item的，而item2vec计算出的embeeding是item-item的，从二者最终的使用方式上便可看出来。其次，二者计算的方式也完全不一样~

至于二者的效果，MF更容易推荐比较热门的内容，而item2vec在时间窗口的基础上更能推荐user最近浏览的相似item。

基于内容

基于内容的推荐方法最好解释，它的思路非常简单，就是建立在“用户经常看什么，我们就给他推荐什么”的思路上。它应该是诞生最早的推荐方法了。
这种方法的一个特点是它的独立性，即给某个用户进行推荐的策略只跟这个用户有关，而与其它用 户的行为无关。

缺点也比较明显，没什么扩展性，且需要已经有一些用户的行为历史。

算法的主要流程为：

1. 给所有的item做分类，或者打标签，早期通过手动或者提取关键字来做，而后可以通过上面介绍的embeding方法来计算相似性来做，或者SVD。
2. 做用户画像，基于用户的长短期行为得到用户感兴趣的分类或者标签。
3. 基于1，2的结果进行推荐

召回方法还有不少，上面介绍的几个只是比较有代表性的几个算法，使用这些算法进行多路召回并合并结果，得到的新的集合，就是我们下一步，排序的输入了。

排序算法

如果说召回决定了我们推荐效果的天花板，那么排序就决定了我们最终逼近天花板的程度。

在文章开头说过，排序阶段一般分成三个步骤：粗排->主排序->重排序。

粗排的原因时因为排序算法一般使用较为复杂的模型，使用较多的参数，速度相对较慢，如果召回阶段产出的item过多，会导致排序时间过长。于是先用一次粗排的过程来缩小样本范围。因此粗排一般使用比较简单的排序方法，比如使用后验CTR(点击率预估)和入库时的预估CTR值直接排序。

主排序则是我们要介绍的学习排序。

重排则是对主排的结果进行一些筛选，比如把结果放到一个类似于session model或者强化学习的模型里面进行重新排序，主要突出用户最近行为的特点。一般来说使用更少的样本范围，比如只把主排序结果的top k进行重排。

所以，最影响排序结果的，还是主排序部分。我们这里介绍的方法也是主排序的方法。

逻辑回归

逻辑回归(logistic regression)这里就不展开来讲了，简单的说就是用函数关系来拟合真实的分布，然后用一个非线性的转换函数将结果拟合成分类结果。

推荐系统中基于一阶特征的逻辑回归如下：

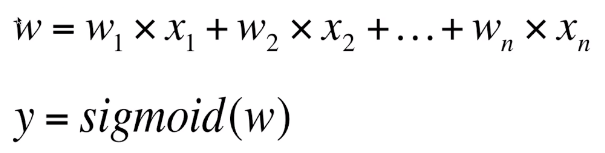
上式的x1,x2,…,xn代表不同的特征，sigmoid是一个可以将函数值映射到0-1间的函数：

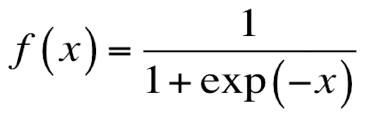
接着再用交叉熵定义损失函数并用梯度下降更新求得w即可。

需要注意的是样本数据的选择和清洗，比如明显的异常数据便应该去掉。
其次，在特征的选取上，那种只有少量数据才拥有的特征意义就不大。

逻辑回归的缺点在于，要想取得好的结果，人工组合的特征不能少，但是人工特征需要不断组合、测试、调优，非常耗费人力，我们能否在模型层面自行进行特征组合呢？

GBDT

单独写一篇文章来讲GBDT。
链接：todo..

GBDT + LR

这个思路来自于《practical lessons from predicting clikcks on ads at facebook》这篇论文。

一句话就可以概括论文的主要想法：
逻辑回归进行融合特征时，一需要手动组合，二调参麻烦，而GBDT这种提升树模型不断用新的决策树学习残差的过程，就相当于不断地把特征变幻成了新的特征，如果把这种高维特征再放入LR模型中去训练，能不能得到更好的结果呢？

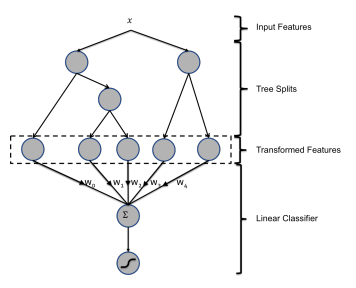
做法也很好实现，先训练好GBDT模型，再把每颗决策树的结果作为新的分类特征，然后使用LR模型进行训练。

看起来有一些trick，但实际效果确实在很多情况下略优于二者。
但2个模型并不是联合训练而是单独进行训练的，二者优化目标不同，从而解释性也就弱了。

FM(factor machine)

由上面的LR模型，我们有了一阶线性模型：

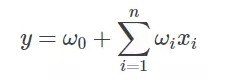
其实很容易想到，想要融入特征组合的概念，我们只需要添加一项：

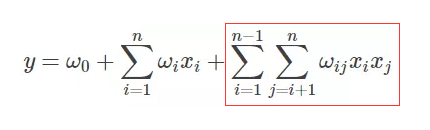
将特征两两组合构成新特征，再次放入线性模型，似乎就在模型层面完成了特征组合了。

其实不然，上诉方法在现实中是很难运用的，因为现实中的数据特征往往非常多，如淘宝京东的商品特征，量级超过千万。
这种情况下，数据矩阵是高度稀疏的，xi,xj同时不为0的可能性非常小，从而使得wij的训练几乎不可能。

FM模型就是一种求解这种高阶稀疏矩阵的方式，它将wij转化成2个向量大小为k的一维向量vi和vj的內积

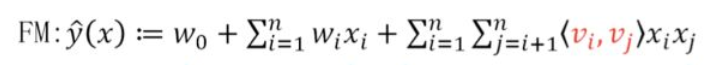
它的本质还是我们上面提到的embedding，为什么它能解决稀疏矩阵的计算问题呢？
因为它的计算并不依赖于xi,xj这种特征组合是否出现，vi的本质是一个embedding, 于某个特征xi而言，只要有足够多xi和其它任何特征一起出现的样本，那么vi就是可以被训练出来的。此时和同样被训练出来的vj计算內积，便可以得到二者组合特征的权重。如下：

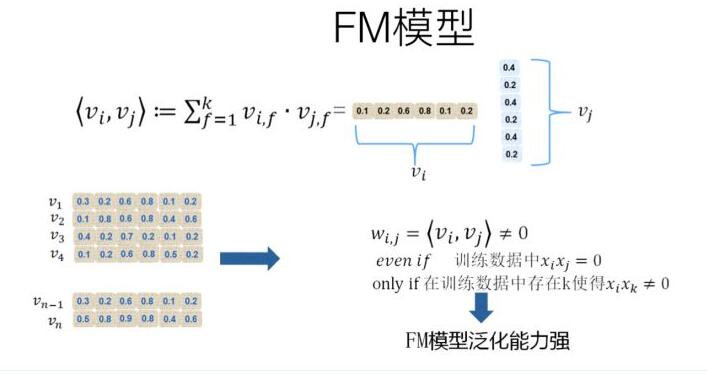
这就是embedding的核心特点，将one-hot或者1-0的硬匹配，转换成了向量间的软匹配，从而能够近似的得到2个本来匹配不上的特征的关系。

公式化简
上诉FM公式中的xixj交叉项是可以化简的，从而更好的进行model serving。

首先，我们要考虑的交叉项肯定不包括自己与自己组合，所以xixi这种情况不考虑，其次xixj,xjxi这种重复的，我们也只算一次。那么原始可以化简如下:

1. 第一步式子中的1/2就是在去重，而减去的项则是自身与自身进行的特征组合。
2. 第二步则是将向量內积展开，k是向量v的维度。
3. 第三步则是先将k求和移到最外层，然后内层是在确定某个特征的第l位的情况下，与其它特征对应的第l位相乘并求和。
4. 第三步到第四步，注意2个求和符号，虽然一个是i，一个是j，但范围相同，求和的对象也相同，所以实际是一样的，直接把乘改为平方即可。

在实际的编码中就很好表示了，Σvilxi就是 样本特征矩阵*v, 最外层的Σ则是求和操作。

再根据实际情况是分类还是回归选择合适的损失函数进行求导即可，因为我们的式子里有常数项、一阶项和二阶交叉项，所以导数也是3个哦~

使用DNN

深度学习在图像和NLP领域都搞得热火朝天如火如荼，那推荐系统可以蹭一蹭吗？答案是可以的，比起上诉的LR,GBDT,FM，神经网络模型最大的优点就是它可以完全自动地对特征进行非线性的组合，且覆盖了二阶组合和高阶组合。

将DNN引入推荐系统，最常用的方法就是wide and deep模型，它来自于google的一篇论文：《Wide & Deep Learning for Recommender Systems》(文末附链接)。

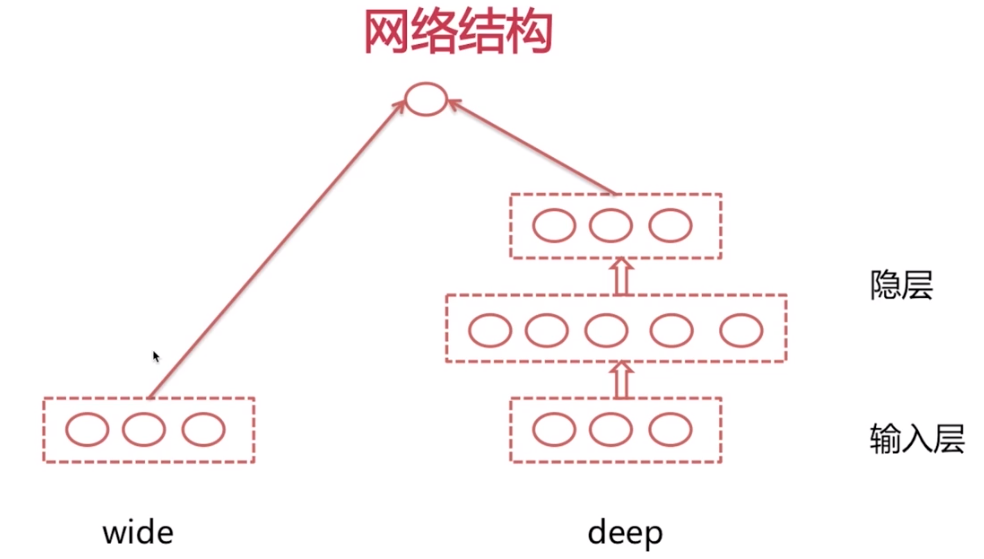
左边的wide部分是一个LR或者FM模型，而右边的deep则是一个神经网络模型，或者说MLP模型。w&d模型的输出是将wide侧输出与deep侧最后一个隐层的输出相加，然后再进行激活得到的。这样做的目的是可以在一次反向传播中同时更新两边的参数，达到联合训练的目的。

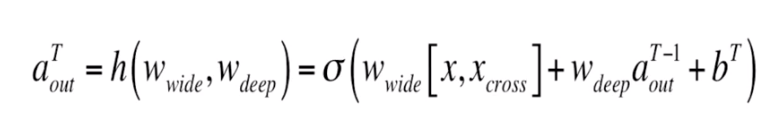
x_cross是组合特征。
Loss目标函数则根据项目的实际情况自行定义，定义好后，再利用神经网络的反向传播进行求解即可。

当然，DNN也有其缺点。而且成也萧何败萧何，上面我们说自动组合特征是DNN的优点，但也是缺点。这种最纯粹的w&d模型，只依靠MLP本身来自动对特征进行组合，但其内里却完全是一个黑盒子，我们并不知道真正组合了什么。

一般来说在实际进行使用的时候，这些排序模型在大规模数据上得到的效果是 w&d>LR+GBDT>GBDT>LR的。
当然，实际情况实际讨论，在模型落地的时候我们都会进行一些符合业务逻辑的修改，或者加入一些其它的想法。所以，选择合适的才是最重要的。

其次，对于实际上线的效果，有很多评估指标，通用的比如AUC、F1，测试集表现等。不同的业务还能根据实际业务定义相应的业务指标。

在特征的选取上，排序阶段则是可以尽量把相关的side info都特征化，毕竟这个阶段的目标就是精确，而更多的信息往往能够得到更好的结果。

总结

再总结一下流程，首先，使用多路召回并合并，从所有item中找到最适合推荐给用户的近千的item。进入排序阶段后，如果item过多导致排序时间长，可以加入粗排阶段，用一些简单的排序模型对召回返回的item进行一次筛选，进一步缩小item范围。接着再使用精确度较高的主排序模型进行精准排序。最后，再根据一些业务策略筛选，比如使实际推荐结果多样化，或者去除已读item等，然后再推荐给用户。

而为了验证模型效果和继续优化模型，我们要继续收集用户的各种行为和反馈。

这些行为和反馈一部分可以实时的用来更新在线推荐模型，让用户的实时行为在下一次刷新中即可得到体现。
而所有这些数据都应该被记录下来补充进我们的离线训练数据，从而用更大的模型进行离线训练，从而周期性地对模型进行更新。

reference

Andrew Ng在coursera上的机器学习课程
word2vec论文:Efficient Estimation of Word Representations in Vector Space
item2vec论文:Item2Vec: Neural Item Embedding for Collaborative Filtering
知乎张俊林专栏：全能的FM模型
gbdt&lr论文：Practical Lessons from Predicting Clicks on Ads at Facebook
wide and deep论文:Wide & Deep Learning for Recommender Systems